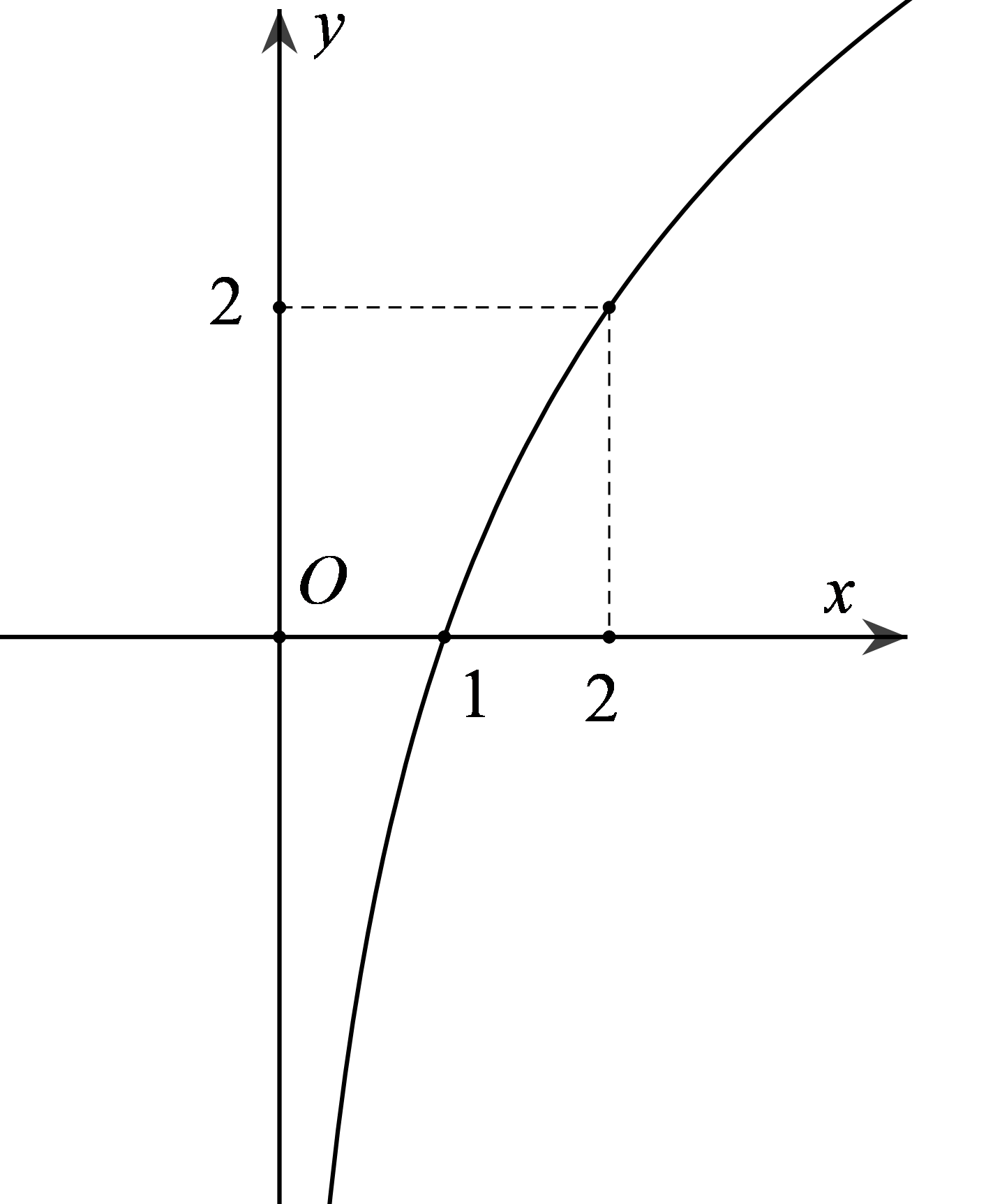Cho hai hàm số \(u\left( x \right)\) và \(v\left( x \right)\) có đạo hàm tại điểm \(x\) thuộc tập xác định. Khẳng định nào dưới đây là đúng?
Quảng cáo
Trả lời:
Đáp án đúng là: C
Cho hai hàm số \(u\left( x \right)\) và \(v\left( x \right)\) có đạo hàm tại điểm \(x\) thuộc tập xác định. Ta có các quy tắc tính đạo hàm:
+ Đạo hàm của tổng: \({\left( {u + v} \right)^\prime } = u' + v'\);
+ Đạo hàm của hiệu: \({\left( {u - v} \right)^\prime } = u' - v'\);
+ Đạo hàm của tích: \({\left( {uv} \right)^\prime } = u'v + uv'\);
+ Đạo hàm của thương: \({\left( {\frac{u}{v}} \right)^\prime } = \frac{{u'v - uv'}}{{{v^2}}}\,\,\,\,\left( {v = v\left( x \right) \ne 0} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
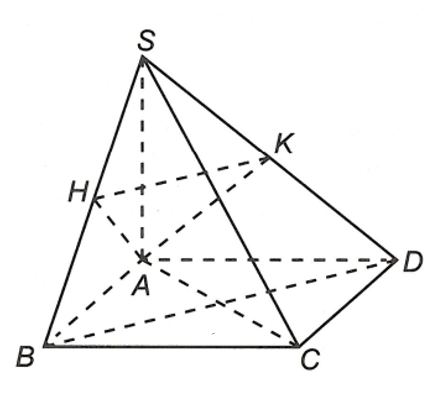
Xét \(\Delta SAB\) vuông tại \(A,\) đường cao \(AH.\)
Ta có \(S{A^2} = SH \cdot SB \Rightarrow \frac{{SH}}{{SB}} = \frac{{S{A^2}}}{{S{B^2}}}\left( 1 \right).\)
Xét \(\Delta SAD\) vuông tại \(A,\) đường cao \(AK.\)
Ta có \(S{A^2} = SK \cdot SD \Rightarrow \frac{{SK}}{{SD}} = \frac{{S{A^2}}}{{S{D^2}}}\left( 2 \right).\)
Mà \(\left\{ \begin{array}{l}S{B^2} = S{A^2} + A{B^2}\\S{D^2} = S{A^2} + A{D^2}\\AB = AD\end{array} \right. \Rightarrow SB = SD\left( 3 \right).\)
Từ \(\left( 1 \right),\left( 2 \right)\) và \(\left( 3 \right)\)suy ra \(\frac{{SH}}{{SB}} = \frac{{SK}}{{SD}} \Rightarrow HK{\rm{//}}BD.\)
Lại có \(BD \bot AC\) (tính chất hình thoi).
Mà \(SA \bot \left( {ABCD} \right),BD \subset \left( {ABCD} \right) \Rightarrow BD \bot SA.\)
Suy ra \(BD \bot \left( {SAC} \right)\) mà \(HK{\rm{//}}BD\) nên \(HK \bot \left( {SAC} \right).\)
Câu 2
Lời giải
Đáp án đúng là: D
Hàm số \(y = {\log _a}x\) \(\left( {0 < a \ne 1} \right)\) có tập xác định là \(D = \left( {0; + \infty } \right)\) nên ta loại ngay đáp án A và đáp án B.
Quan sát hình vẽ ta thấy đồ thị hàm số đi lên từ trái qua phải trên \(\left( {0; + \infty } \right)\) nên hàm số này đồng biến trên \(\left( {0; + \infty } \right)\), vậy ta chọn đáp án D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.