(4,0 điểm)
Trong chuyện ngụ ngôn La Phông ten, Cò mời Cáo đến ăn tiệc với món súp hảo hạng. Món súp đó Cò thường cho vào một cái bình hình trụ, có bán kính đáy là \[4\]\[cm\], chiều cao \[30\,\,cm.\] Nhưng khi Cáo đến Cò chỉ đổ súp sao cho phần súp trong bình đó cao \[10\,\,cm\]và mời Cáo dùng bữa.
a) Tính thể tích của phần súp mà Cò mời Cáo ăn.
b) Cổ của Cáo quá ngắn nên không thể lấy được súp, Cáo nhìn quanh và phát hiện ra nhà Cò có những viên sỏi hình cầu giống hệt nhau, bán kính là \[2\,\,cm.\] Cáo bèn cho từng viên sỏi vào bình súp đến khi súp dâng lên vừa đầy đến miệng bình rồi Cáo thảnh thơi ăn súp. Hỏi Cáo đã cho vào bình bao nhiêu viên bi.
(4,0 điểm)
Trong chuyện ngụ ngôn La Phông ten, Cò mời Cáo đến ăn tiệc với món súp hảo hạng. Món súp đó Cò thường cho vào một cái bình hình trụ, có bán kính đáy là \[4\]\[cm\], chiều cao \[30\,\,cm.\] Nhưng khi Cáo đến Cò chỉ đổ súp sao cho phần súp trong bình đó cao \[10\,\,cm\]và mời Cáo dùng bữa.
a) Tính thể tích của phần súp mà Cò mời Cáo ăn.
b) Cổ của Cáo quá ngắn nên không thể lấy được súp, Cáo nhìn quanh và phát hiện ra nhà Cò có những viên sỏi hình cầu giống hệt nhau, bán kính là \[2\,\,cm.\] Cáo bèn cho từng viên sỏi vào bình súp đến khi súp dâng lên vừa đầy đến miệng bình rồi Cáo thảnh thơi ăn súp. Hỏi Cáo đã cho vào bình bao nhiêu viên bi.
Quảng cáo
Trả lời:
a) Thể tích của phần súp mà Cò mời Cáo ăn là \({V_1} = \pi \cdot {4^2} \cdot 10 = 160\pi \,\,(c{m^3})\)
Vậy thể tích của phần súp mà Cò mời Cáo ăn là \(480\pi \,\,(c{m^3})\)
b) Thể tích của bình hình trụ đó là \({V_0} = \pi \cdot {4^2} \cdot 30 = 480\pi \,\,(c{m^3})\)
khi Cáo thả những viên bi vào thì súp dâng đến vừa đầy miệng bình nên thể tích của các viên bi là \(V = {V_0} - {V_1} = 480\pi - 160\pi = 320\pi \,\,(c{m^3})\)
Thể tích của mỗi viên bi là \[{V_{1\,vien\,bi}} = \frac{4}{3}\pi .{R^3} = \frac{4}{3}\pi {.2^3} = \frac{{32}}{3}\pi \] (cm3)
Số lượng viên sỏi đã thêm vào là: \[320\pi :\left( {\frac{{32}}{3}\pi } \right) = 30\] (viên)
Vậy Cáo đã thêm \(30\) viên bi.
Câu hỏi cùng đoạn
Câu 2:
Cho nửa đường tròn tâm \[O\], bán kính \[AB = 2R\]và tia tiếp tuyến \[Ax\] cùng phía với nửa đường tròn đối với \[AB.\] Từ điểm \[M\] trên \[Ax\] kẻ tiếp tuyến thứ hai \[MC\]với nửa đường tròn ( \[C\] là tiếp điểm). \[AC\] cắt \[OM\] tại E ; \[MB\] cắt nửa đường tròn (O) tại \[D\] (\(D \ne B\)).
a) Chứng minh rằng bốn điểm \[A,M,C,O\] cùng thuộc một đường tròn.
b) Tính diện tích hình quạt \[OCB\] theo \[R\], trong trường hợp \(\widehat {AMC} = {60^ \circ }\) và chứng minh
\(\widehat {ADE} = \widehat {ACO}\).
c) Gọi \[H\] là hình chiếu của \[C\]trên \[AB.\]Chứng minh rằng \[MB\] đi qua trung điểm của \[CH\].
Cho nửa đường tròn tâm \[O\], bán kính \[AB = 2R\]và tia tiếp tuyến \[Ax\] cùng phía với nửa đường tròn đối với \[AB.\] Từ điểm \[M\] trên \[Ax\] kẻ tiếp tuyến thứ hai \[MC\]với nửa đường tròn ( \[C\] là tiếp điểm). \[AC\] cắt \[OM\] tại E ; \[MB\] cắt nửa đường tròn (O) tại \[D\] (\(D \ne B\)).
a) Chứng minh rằng bốn điểm \[A,M,C,O\] cùng thuộc một đường tròn.
b) Tính diện tích hình quạt \[OCB\] theo \[R\], trong trường hợp \(\widehat {AMC} = {60^ \circ }\) và chứng minh
\(\widehat {ADE} = \widehat {ACO}\).
c) Gọi \[H\] là hình chiếu của \[C\]trên \[AB.\]Chứng minh rằng \[MB\] đi qua trung điểm của \[CH\].
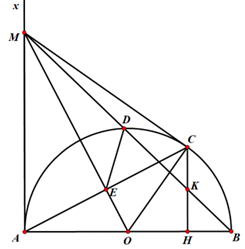
a) Do \[MA,MB\] là tiếp tuyến của nửa đương tròn (O) nên ta có \(\widehat {MAO} = \widehat {MCO} = {90^ \circ }\)
Suy ra là tam giác vuông tại \(A\) và là tam giác vuông tại \(C\)
Suy ra \[M,A,O\] cùng thuộc đường tròn đường kính \[MO\] và \[M,C,O\] cùng thuộc đường tròn đường kính \[MO\]
Do đó bốn điểm \[A,M,C,O\] cùng thuộc một đường tròn.
b) Ta có \(\widehat {AMC} = \widehat {COB} = {60^ \circ }\) ( hai góc cùng bù với \(\widehat {AOC}\))
Diện tích hình quạt \(COB\) là \(\frac{{60}}{{360}}\pi \cdot {R^2} = \frac{{\pi {R^2}}}{6}\)
Do \[MA,MC\]là hai tiếp tuyến của nửa đường tròn (O) nên \[MA = MC\]và \[OA = OC\]
Từ đó suy ra \[M\] thuộc đường trung trực của \[AC,O\] thuộc đường trung trực của \[AC\]
Nên \[MO\] vuông góc \[AC\]tại trung điểm \[E\] của \[AC\], suy ra \(\widehat {AEM} = {90^ \circ }\)
Suy ra vuông tại \(E\), nên nội đường tròn đường kính \[MA\]
Có \(\widehat {ADM} = 180 - \widehat {ADB} = {90^ \circ }\) ( do \(\widehat {ADB}\) chắn nửa đường tròn nên \(\widehat {ADB} = {90^ \circ }\)).
Suy ra \(\Delta ADM\) vuông tại \(D\), nên \(\Delta ADM\) nội đường tròn đường kính \[MA\]
Do đó tứ giác \(AMDE\) nội tiếp đường tròn đường kính \[MA\].
Xét tứ giác \(AMDE\) nội tiếp có :\(\widehat {ADE} = \widehat {AMO}\) (cùng chắn )
Xét tứ giác \(AMCO\) nội tiếp có :\(\widehat {AMO} = \widehat {ACO}\) (cùng chắn )
Suy ra \(\widehat {ADE} = \widehat {ACO}\).
c) Gọi \(K\) là giao điểm của \(MB\) và \(CH\).
Do \(CH//AM\) nên theo định lí Thales thì \(\frac{{HK}}{{AM}} = \frac{{HB}}{{AB}} = \frac{{HB}}{{2R}} = \frac{1}{2} \cdot \frac{{HB}}{R}\)
Ta có \[OM//BC\]( cùng vuông góc với \[AC\]) suy ra \(\widehat {MOA} = \widehat {CBH}\) ( hai góc đồng vị)
Xét \(\Delta HCB\) và \(\Delta AMO\) có \(\widehat {MAO} = \widehat {CHB} = {90^ \circ }\) ; \(\widehat {MOA} = \widehat {CBH}\)
Suy ra \(\Delta HCB \sim \Delta AMO\), nên \(\frac{{HB}}{{OA}} = \frac{{CH}}{{AM}} = \frac{{HB}}{R}\)
Do đó \(\frac{{HK}}{{AM}} = \frac{1}{2} \cdot \frac{{CH}}{{AM}}\) hay \(HK = \frac{1}{2}CH\)
Suy ra \[MB\] đi qua trung điểm của \[CH\] (đpcm).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số tình nguyện viên đội \[A\] là \(x\)(đơn vị: tình nguyện viên)
số tình nguyện viên đội \[B\] là \(y\) (đơn vị: tình nguyện viên)
Điều kiện: \(x;y \in {\mathbb{N}^*};x;y < 27\)
Theo đề bài ta có phương trình \(x + y = 27\quad \left( 1 \right)\)
Số cây đội A trồng được là \(2x\) (cây xanh)
Số cây đội B trồng được là \(3y\) (cây xanh)
Theo đề bài ta có phương trình \(2x + 3y = 66\quad \left( 2 \right)\)
Từ \(\left( 1 \right)\)và \(\left( 2 \right)\)ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 27\\2x + 3y = 66\end{array} \right.\)
Giải hệ ta được \(\left\{ \begin{array}{l}x = 15\\y = 12\end{array} \right.\)(thỏa mãn điều kiện)
Vậy đội A có \(15\)tình nguyện viên và đội B có \(12\) tình nguyện viên
Lời giải
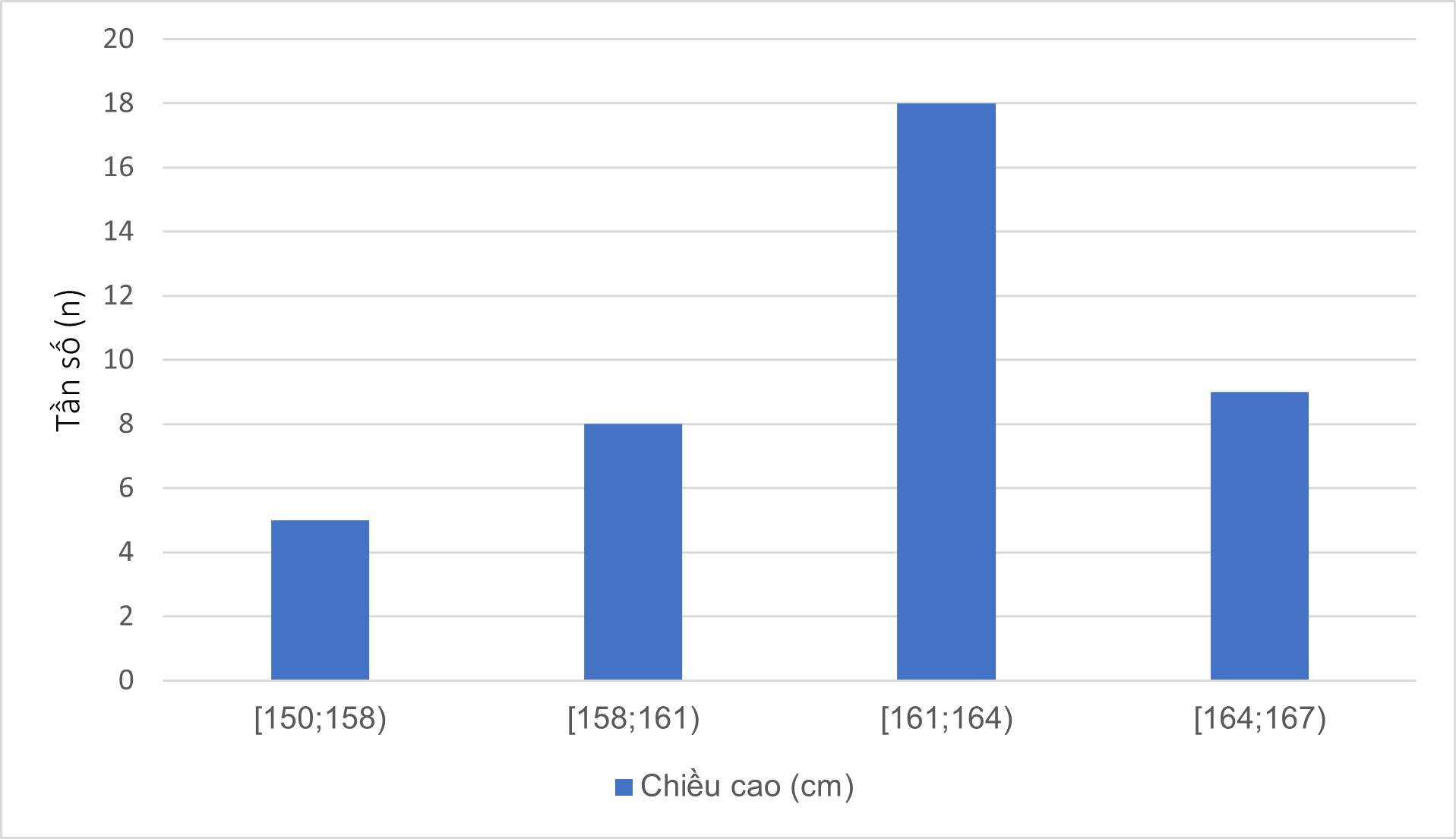
Tần số ghép nhóm của nhóm \([161;164)\) là \(n = 18\).
Tần số tương đối ghép nhóm của nhóm \([161;164)\) là: \(f = \frac{{18.100}}{{40}}\% = 45\% \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.