(1,5 điểm)
Sau khi thống kê chiều cao của \(40\) học sinh lớp 9A, cô giáo lập biểu đồ tần số ghép nhóm dưới đây:
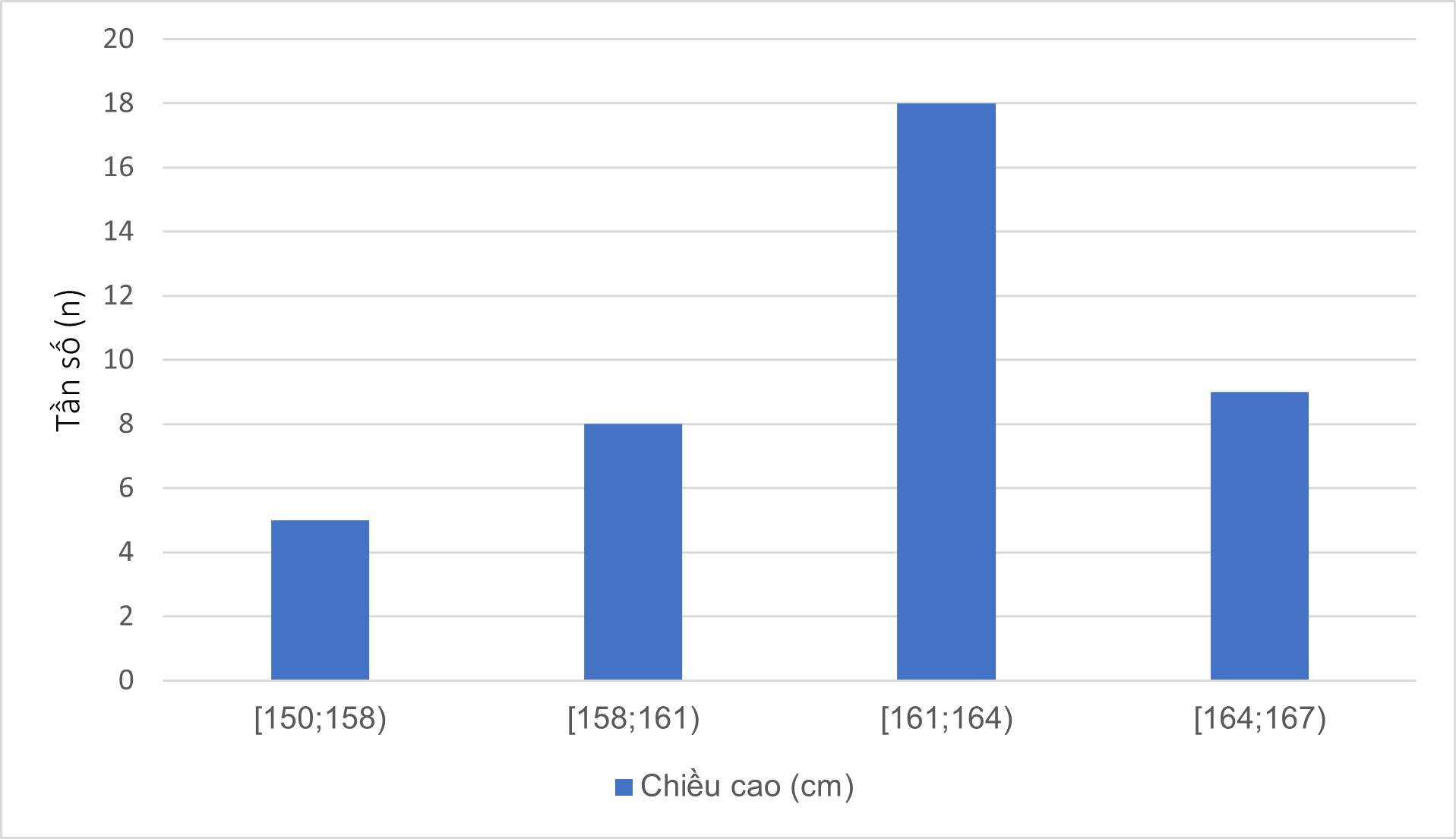
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm \([161;164)\).
Sau khi thống kê chiều cao của \(40\) học sinh lớp 9A, cô giáo lập biểu đồ tần số ghép nhóm dưới đây:
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm \([161;164)\).
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 16 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Tần số ghép nhóm của nhóm \([161;164)\) là \(n = 18\).
Tần số tương đối ghép nhóm của nhóm \([161;164)\) là: \(f = \frac{{18.100}}{{40}}\% = 45\% \)
Câu hỏi cùng đoạn
Câu 2:
Một hộp chứa \(9\) quả bóng màu cam và một số quả bóng màu trắng. Các quả bóng có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên một quả bóng từ hộp, xem màu rồi trả lại hộp. Biết xác suất của biến cố "Lấy được quả bóng màu trắng" là \(\frac{2}{5}\). Hỏi trong hộp có bao nhiêu quả bóng màu trắng?
Một hộp chứa \(9\) quả bóng màu cam và một số quả bóng màu trắng. Các quả bóng có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên một quả bóng từ hộp, xem màu rồi trả lại hộp. Biết xác suất của biến cố "Lấy được quả bóng màu trắng" là \(\frac{2}{5}\). Hỏi trong hộp có bao nhiêu quả bóng màu trắng?
Giải bởi Vietjack
Gọi số quả bóng trắng trong hộp là \(x\) (đơn vị: quả bóng) \(\left( {x \in {\mathbb{N}^*}} \right)\)
Tổng số quả bóng trong hộp là \(9 + x\)(quả bóng)
Xác suất để lấy được một quả bóng màu trắng là: \(P = \frac{x}{{x + 9}}\)
Theo đề bài, ta có phương trình: \[\frac{x}{{x + 9}} = \frac{2}{5}\]
\[5x = 2\left( {x + 9} \right)\]
\[x = 6\] (thỏa mãn điều kiện)
Vậy trong hộp có \(6\)quả bóng màu trắng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Thể tích của phần súp mà Cò mời Cáo ăn là \({V_1} = \pi \cdot {4^2} \cdot 10 = 160\pi \,\,(c{m^3})\)
Vậy thể tích của phần súp mà Cò mời Cáo ăn là \(480\pi \,\,(c{m^3})\)
b) Thể tích của bình hình trụ đó là \({V_0} = \pi \cdot {4^2} \cdot 30 = 480\pi \,\,(c{m^3})\)
khi Cáo thả những viên bi vào thì súp dâng đến vừa đầy miệng bình nên thể tích của các viên bi là \(V = {V_0} - {V_1} = 480\pi - 160\pi = 320\pi \,\,(c{m^3})\)
Thể tích của mỗi viên bi là \[{V_{1\,vien\,bi}} = \frac{4}{3}\pi .{R^3} = \frac{4}{3}\pi {.2^3} = \frac{{32}}{3}\pi \] (cm3)
Số lượng viên sỏi đã thêm vào là: \[320\pi :\left( {\frac{{32}}{3}\pi } \right) = 30\] (viên)
Vậy Cáo đã thêm \(30\) viên bi.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi số tình nguyện viên đội \[A\] là \(x\)(đơn vị: tình nguyện viên)
số tình nguyện viên đội \[B\] là \(y\) (đơn vị: tình nguyện viên)
Điều kiện: \(x;y \in {\mathbb{N}^*};x;y < 27\)
Theo đề bài ta có phương trình \(x + y = 27\quad \left( 1 \right)\)
Số cây đội A trồng được là \(2x\) (cây xanh)
Số cây đội B trồng được là \(3y\) (cây xanh)
Theo đề bài ta có phương trình \(2x + 3y = 66\quad \left( 2 \right)\)
Từ \(\left( 1 \right)\)và \(\left( 2 \right)\)ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 27\\2x + 3y = 66\end{array} \right.\)
Giải hệ ta được \(\left\{ \begin{array}{l}x = 15\\y = 12\end{array} \right.\)(thỏa mãn điều kiện)
Vậy đội A có \(15\)tình nguyện viên và đội B có \(12\) tình nguyện viên
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập