(2,5 điểm)
Hưởng ứng chiến dịch mùa hè xanh, \(27\)tình nguyện viên chia thành hai đội tham gia trồng cây gây rừng. Mỗi tình nguyện viên đội \[A\] trồng được \(2\)cây xanh. Mỗi tình nguyện viên đội \[B\] trồng được \(3\)cây xanh. Tổng kết phong trào cả hai đội trồng được \(66\) cây. Tính số tình nguyện viên mỗi đội.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 16 !!
Quảng cáo
Trả lời:
Gọi số tình nguyện viên đội \[A\] là \(x\)(đơn vị: tình nguyện viên)
số tình nguyện viên đội \[B\] là \(y\) (đơn vị: tình nguyện viên)
Điều kiện: \(x;y \in {\mathbb{N}^*};x;y < 27\)
Theo đề bài ta có phương trình \(x + y = 27\quad \left( 1 \right)\)
Số cây đội A trồng được là \(2x\) (cây xanh)
Số cây đội B trồng được là \(3y\) (cây xanh)
Theo đề bài ta có phương trình \(2x + 3y = 66\quad \left( 2 \right)\)
Từ \(\left( 1 \right)\)và \(\left( 2 \right)\)ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 27\\2x + 3y = 66\end{array} \right.\)
Giải hệ ta được \(\left\{ \begin{array}{l}x = 15\\y = 12\end{array} \right.\)(thỏa mãn điều kiện)
Vậy đội A có \(15\)tình nguyện viên và đội B có \(12\) tình nguyện viên
Câu hỏi cùng đoạn
Câu 2:
Lúc \(6\) giờ \(30\) phút, một ca nô xuôi dòng sông từ \[A\] đến \[B\] dài \(48\)km. Khi đến \[B\], ca nô nghỉ \(30\) phút sau đó lại ngược dòng từ \[B\] về \[A\] lúc \(10\) giờ \(36\) phút cùng ngày. Tìm vận tốc riêng của ca nô, biết vận tốc dòng nước là \(3\)km/h.
Gọi vận tốc riêng của ca nô là \(x\)(đơn vị: km/h) \(\left( {x > 3} \right)\)
Vận tốc ca nô đi xuôi dòng là \(x + 3\)(km/h)
Vận tốc ca nô đi ngược dòng là \(x - 3\)(km/h)
Thời gian ca nô đi xuôi dòng là \(\frac{{48}}{{x + 3}}\)(h)
Thời gian ca nô đi ngược dòng là \(\frac{{48}}{{x - 3}}\)(h)
Theo đề bài ta có phương trình \(\frac{{48}}{{x + 3}} + \frac{1}{2} + \frac{{48}}{{x - 3}} = \frac{{41}}{{10}}\)
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{48}}{{x + 3}} + \frac{{48}}{{x - 3}} = \frac{{18}}{5}\\\frac{{48\left( {x - 3} \right) + 48\left( {x + 3} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} = \frac{{18}}{5}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{96x}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} = \frac{{18}}{5}\\\,\,\,\,\,\,\,\,\,\,\,\,\,3{x^2} - 80x - 27 = 0\\\,\,\,\,\,\,\,\,\,\,\,\left( {3x + 1} \right)\left( {x - 27} \right) = 0\end{array}\)
\(x = \frac{{ - 1}}{3}\) (loại) hoặc \(x = 27\)(thoả mãn)
Vậy vận tốc riêng của ca nô là \(27km/h\).
Câu 3:
Phương trình \({x^2} - 2x - m + 1 = 0\) (\(m\)là tham số) có một nghiệm là \(x = 1 + \sqrt 7 \). Tính giá trị của biểu thức \(A = x_1^2{x_2} + x_2^2{x_1}\).
Thay \(x = 1 + \sqrt 7 \)vào phương trình ta có: \({\left( {1 + \sqrt 7 } \right)^2} - 2\left( {1 + \sqrt 7 } \right) - m + 1 = 0\)
\(8 + 2\sqrt 7 - 2 - 2\sqrt 7 - m + 1 = 0\)
\(m = 7\)
Phương trình có dạng \({x^2} - 2x - 6 = 0\)
Áp dụng hệ thức Vi – ét ta có: \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2}\\{{x_1}.{x_2} = - 6}\end{array}} \right.\)
Ta có \(A = x_1^2{x_2} + x_2^2{x_1} = {x_1}{x_2}\left( {{x_1} + {x_2}} \right) = - 6 \cdot 2 = - 12\)
Vậy \(A = - 12\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi chiều rộng của hình chữ nhật đáy bể là \(x\)(m) (điều kiện \(x > 0\))
Suy ra chiều dài của hình chữ nhật là \(4x\)(m).
Gọi \(y\) là chiều cao của bể (điều kiện \(y > 0\))
Nên ta có \[V = 4x.x.y = 400 \Leftrightarrow {x^2}.y = 100 \Leftrightarrow y = \frac{{100}}{{{x^2}}}\].
Diện tích xây dựng của bể là \[S = 4{x^2} + 2\left( {x + 4x} \right)y = 4{x^2} + 10xy = 4{x^2} + 10.\frac{{100}}{{{x^2}}}.x = 4{x^2} + \frac{{1000}}{x}\]Áp dụng bất đẳng thức \[AM - GM\] ta có: \[S = 4{x^2} + \frac{{1000}}{x} = \left( {4{x^2} + 100} \right) + \frac{{1000}}{x} - 100 \ge 2\sqrt {4{x^2}.100} + \frac{{1000}}{x} - 100 = 40x + \frac{{1000}}{x} - 100\]Và \[S \ge 40x + \frac{{1000}}{x} - 100 \ge 2\sqrt {40x.\frac{{1000}}{x}} - 100 = 400 - 100 = 300\].
Khi đó \({S_{\min }} = 300\).
Dấu = xảy ra khi \[\left\{ {\begin{array}{*{20}{c}}{4{x^2} = 100}\\{40x = \frac{{1000}}{x}}\end{array}} \right. \Leftrightarrow x = 5\].
Vậy chi phí thấp nhất thuê nhân công là \[300.500000 = 150000000\] đồng \( = 150\)triệu đồngLời giải
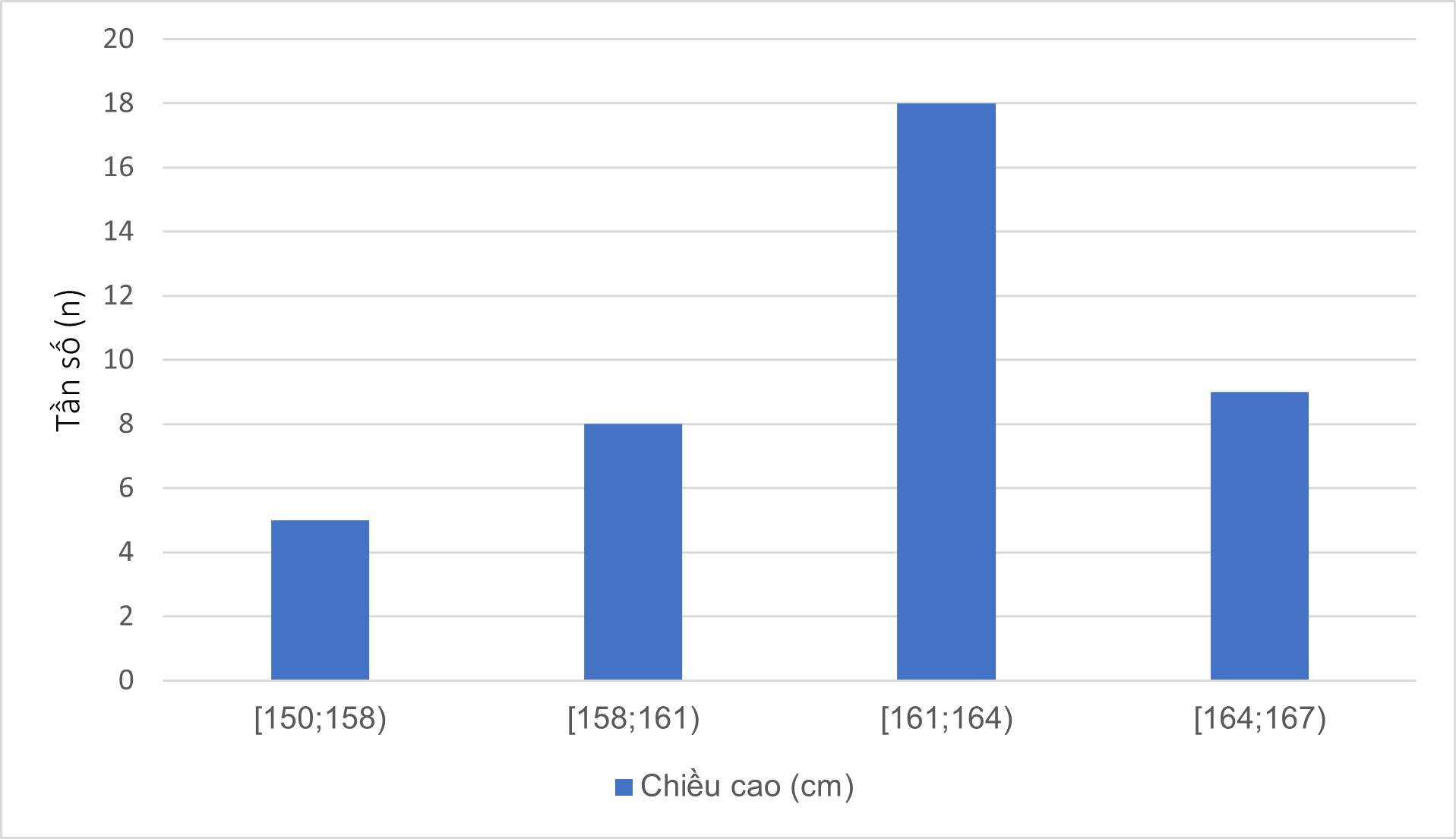
Tần số ghép nhóm của nhóm \([161;164)\) là \(n = 18\).
Tần số tương đối ghép nhóm của nhóm \([161;164)\) là: \(f = \frac{{18.100}}{{40}}\% = 45\% \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.