a) Hai bạn An và Nam cùng mang số tiền như nhau đến nhà sách để mua tập. An mua loại tập giá \(11\,000\)đồng một quyển, Nam mua loại tập giá \(12\,000\) đồng một quyển. Khi đến nhà sách, hai bạn mới biết nhân dịp “Ngày sách và văn hóa đọc Việt Nam năm \(2023\)” nhà sách có chương trình giảm giá cho các loại tập, sách, văn phòng phẩm,… trong đó có giảm giá \(20\% \) cho các loại tập. Vì thế, số tập của bạn An mua được nhiều hơn số tập của bạn Nam mua là \(2\) quyển. Tính số tập của mỗi bạn đã mua và số tiền mỗi bạn phải trả.
b) Cho hàm số \(y = - {x^2}\) có đồ thị \(\left( P \right)\). Hãy vẽ đồ thị \(\left( P \right)\) và tìm tọa độ giao điểm của \(\left( P \right)\) với đường thẳng \(\left( d \right):y = 2x\).
a) Hai bạn An và Nam cùng mang số tiền như nhau đến nhà sách để mua tập. An mua loại tập giá \(11\,000\)đồng một quyển, Nam mua loại tập giá \(12\,000\) đồng một quyển. Khi đến nhà sách, hai bạn mới biết nhân dịp “Ngày sách và văn hóa đọc Việt Nam năm \(2023\)” nhà sách có chương trình giảm giá cho các loại tập, sách, văn phòng phẩm,… trong đó có giảm giá \(20\% \) cho các loại tập. Vì thế, số tập của bạn An mua được nhiều hơn số tập của bạn Nam mua là \(2\) quyển. Tính số tập của mỗi bạn đã mua và số tiền mỗi bạn phải trả.
b) Cho hàm số \(y = - {x^2}\) có đồ thị \(\left( P \right)\). Hãy vẽ đồ thị \(\left( P \right)\) và tìm tọa độ giao điểm của \(\left( P \right)\) với đường thẳng \(\left( d \right):y = 2x\).Quảng cáo
Trả lời:
Giải bởi Vietjack
a)Gọi \(x,\,y\) lần lượt là số tập của bạn An và bạn Nam mua (\(x,\,y \in {\mathbb{N}^*}\))
Ta có phương trình: \(x - y = 2\)
Sau giảm giá \(20\% \), giá mỗi quyển tập bạn An là
\(\left( {1 - 20\% } \right).11\,000 = 8\,800\) (đồng)
Số tiền mua tập của An là: \(8\,800x\) (đồng)
Sau giảm giá \(20\% \), giá mỗi quyển tập bạn Nam là
\(\left( {1 - 20\% } \right).12\,000 = 9\,600\) (đồng)
Số tiền mua tập của Nam là: \(9\,600y\) (đồng)
Ta có phương trình: \(8\,800x = 9600y\)
Ta có hệ phương trình:\(\left\{ \begin{array}{l}x - y = 2\\8\,800x - 9600y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 24\\y = 22\end{array} \right.\)
Vậy số tập của bạn An và bạn Nam mua lần lượt là \(24\) quyển, \(22\) quyển.
Số tiền mỗi bạn phải trả là \(24 \times 8\,\,800 = 211{\rm{ }}200\)(đồng)
b)Bảng giá trị
\(x\).\(0\).\(1\).\(2\)
\(y\).\(0\).\( - 1\).\( - 4\)
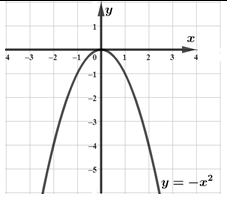
Phương trình hoành độ giao điểm \( - {x^2} = 2x \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 0\\x = - 2 \Rightarrow y = - 4\end{array} \right.\)
Vậy toạ độ giao điểm là \(\left( {0;0} \right)\) và \(\left( { - 2; - 4} \right)\).
(Tìm toạ độ giao điểm bằng đồ thị vẫn cho điểm tối đa)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)
Suy ra tứ giác \(AMCO\) nội tiếp đường tròn.
b)Gọi \(N\) là giao điểm của tiếp tuyến tại \(C\) và \(B\).
Theo tính chất tiếp tuyến ta có \(MC = MA,NC = NB\).
Vì \(CI||NB\) nên theo định lí Thalet ta có
\(\frac{{CI}}{{NB}} = \frac{{MC}}{{MN}}\) và \(\frac{{CN}}{{NM}} = \frac{{IB}}{{BM}}\) (1)
\( \Rightarrow \frac{{CI}}{{MC}} = \frac{{NB}}{{MN}} = \frac{{CN}}{{MN}}\) (2)
Vì \(IH||AM\) nên theo định lí Thalet ta có
\(\frac{{IH}}{{AM}} = \frac{{BI}}{{BM}}\) (3)
Từ (1), (2) và (3) ta có \(\frac{{CI}}{{MC}} = \frac{{IH}}{{MA}} \Rightarrow CI = IH \Rightarrow \)\(I\)là trung điểm của \(CH\).
Lời giải
a) Giải phương trình \(x\left( {x - 4} \right) + 3 = 0.\)
\(x\left( {x - 4} \right) + 3 = 0 \Leftrightarrow {x^2} - 4x + 3 = 0\)
Do \(a + b + c = 0\)
Nên phương trình có nghiệm \(x = 1\)
và nghiệm còn lại \(x = \frac{c}{a} = 3.\)
b) Cho phương trình \[{x^2} - 5x - 14 = 0\] có hai nghiệm phân biệt \[{x_1},{\rm{ }}{x_2}\]. Không giải phương trình, tính giá trị của biểu thức \[P = \frac{{{x_1} + 1}}{{{x_2}}} + \frac{{{x_2} + 1}}{{{x_1}}} \cdot \]
Theo định lí Viet ta có \[\left\{ \begin{array}{l}{x_1} + {x_2} = 5\\{x_1}{x_2} = - 14\end{array} \right.\]
\(P = \frac{{{x_1}\left( {{x_1} + 1} \right) + {x_2}\left( {{x_2} + 1} \right)}}{{{x_1}{x_2}}}\)
\(P = \frac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2} + \left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2}}}\)
\(P = \frac{{{5^2} + 28 + 5}}{{ - 14}} = - \frac{{29}}{7}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập