(4,0 điểm)
Hộp phô mai hình trụ có đường kính đáy \({\rm{10}}{\rm{,6}}\,{\rm{cm}}\) và chiều cao \({\rm{1}}{\rm{,5}}\,{\rm{cm}}\).
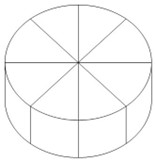
a) Biết rằng 8 miếng phô mai được xếp nằm sát bên trong hộp. Hỏi thể tích của một miếng phô mai là bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất, lấy\(\pi \approx 3,14\))
b) Người ta gói từng miếng phô mai bằng loại giấy đặc biệt. Giả sử phần miếng phô mai được gói chiếm 90% diện tích giấy gói. Em hãy tính diện tích giấy gói được sử dụng cho một miếng phô mai.
Hộp phô mai hình trụ có đường kính đáy \({\rm{10}}{\rm{,6}}\,{\rm{cm}}\) và chiều cao \({\rm{1}}{\rm{,5}}\,{\rm{cm}}\).

b) Người ta gói từng miếng phô mai bằng loại giấy đặc biệt. Giả sử phần miếng phô mai được gói chiếm 90% diện tích giấy gói. Em hãy tính diện tích giấy gói được sử dụng cho một miếng phô mai.
Quảng cáo
Trả lời:
Hộp phô mai hình trụ có đường kính đáy \({\rm{10}}{\rm{,6}}\,{\rm{cm}}\) và chiều cao \({\rm{1}}{\rm{,5}}\,{\rm{cm}}\).
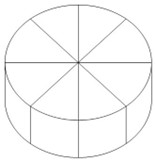
a) Biết rằng 8 miếng phô mai được xếp nằm sát bên trong hộp. Hỏi thể tích của một miếng phô mai là bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất, lấy\(\pi \approx 3,14\))
Thể tích hộp phô mai là:\[V = h.\frac{1}{4}.\pi .{d^2} \approx 1,5.\frac{1}{4}{.3,14.10,6^2} = 132,3039\,(c{m^3})\].
Thể tích một miếng phô mai là: \[V' = \frac{{132,3039}}{8} \approx 16,5\,(c{m^3})\].
b) Diện tích xung quanh của một miếng phô mai là:
\[S = 2 \cdot \frac{d}{2} \cdot h + \frac{{d \cdot \pi \cdot h}}{8} + 2 \cdot \frac{{\frac{1}{4} \cdot \pi \cdot {d^2}}}{8}\]
\( \approx 10,6 \cdot 1,5 + \frac{{10,6 \cdot 3,14 \cdot 1,5}}{8} + \frac{{3,14 \cdot {{10,6}^2}}}{{16}} = 44,70815\,(c{m^2})\)
Diện tích giấy gói được sử dụng cho một miếng phô mai là:
\(\;\;\;\;\;\;\;\;\;\;\;\;\;S' = 44,70815:90\% \approx 49,7\,(c{m^2})\).
Câu hỏi cùng đoạn
Câu 2:
Cho tam giác \[ABC\] có ba góc nhọn nội tiếp đường tròn tâm \[O\] bán kính \[R\]và \[AH\] là đường cao của tam giác \[ABC\]. Gọi \[M,\,N\] lần lượt là chân đường vuông góc kẻ từ \[H\] đến \[AB\] và \[AC\].
a) Chứng minh bốn điểm \[A,\,M,\,H,\,N\]cùng thuộc một đường tròn.
b) Chứng minh \[\widehat {ABC} = \widehat {ANM}\] và \[OA\]vuông góc với \[MN\].
c) Cho biết\[AH = R\sqrt 2 \], chứng minh \[M,\,O,N\]thẳng hàng.
Cho tam giác \[ABC\] có ba góc nhọn nội tiếp đường tròn tâm \[O\] bán kính \[R\]và \[AH\] là đường cao của tam giác \[ABC\]. Gọi \[M,\,N\] lần lượt là chân đường vuông góc kẻ từ \[H\] đến \[AB\] và \[AC\].
a) Chứng minh bốn điểm \[A,\,M,\,H,\,N\]cùng thuộc một đường tròn.
b) Chứng minh \[\widehat {ABC} = \widehat {ANM}\] và \[OA\]vuông góc với \[MN\].
c) Cho biết\[AH = R\sqrt 2 \], chứng minh \[M,\,O,N\]thẳng hàng.
a)
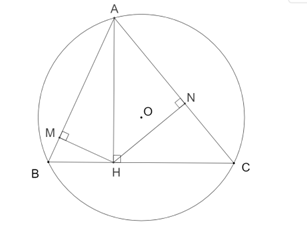
Ta có \[HM \bot AB\]tại \[M\]nên \[\Delta AMH\] vuông tại \[M\], suy ra \[A,\,M,\,H\] cùng thuộc đường tròn đường kính \[AH\].
Ta có \[HN \bot AC\]tại \[N\]nên \[\Delta ANH\]vuông tại \[N\], suy ra \[A,\,N,\,H\]cùng thuộc đường tròn đường kính \[AH\].
Do đó 4 điểm \[A,\,M,\,H,\,N\]cùng thuộc đường tròn đường kính AH.
b)
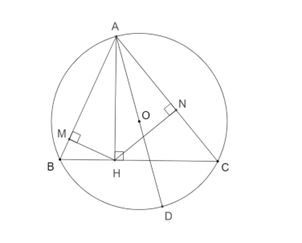
Xét \[\Delta AMH\] và \[\Delta AHB\] có \(\widehat {AMH} = \widehat {AHB} = 90^\circ \), \[\widehat A\] chung
\[ \Rightarrow \] \[ \Rightarrow \] \(\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}\)
\[ \Rightarrow \]\[A{H^2} = AM.AB(1)\]
Chứng minh tương tự có \[A{H^2} = AN.AC(2)\]
Từ (1) và (2) suy ra \[AM.AB = AN.AC\]\[ \Rightarrow \] \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\)
Xét \[\Delta AMN\] và \[\Delta ACB\]: \(\left\{ {\begin{array}{*{20}{c}}{\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}}\\{\hat A\;chung}\end{array}} \right.\)
\(\)\[ \Rightarrow \] \[ \Rightarrow \]\(\widehat {ANM} = \widehat {ABC}\) (hai góc tương ứng) (3)
Kẻ đường kính \[AD\] ta có \(\widehat {DAC} = \widehat {DBC}\) (hai góc nội tiếp cùng chắn cung \[DC\]) (4)
Từ \[(3);(4)\] suy ra \(\widehat {ANM} + \widehat {DAC} = \widehat {ABC} + \widehat {DBC} = \widehat {ABD} = 90^\circ \)
\[ \Rightarrow AO \bot MN\]
c) 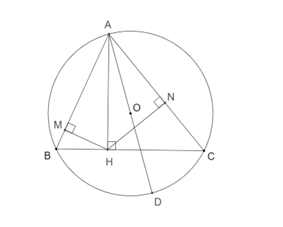
Theo chứng minh trên có \[AN.AC = A{H^2} = 2{R^2} = AO.AD\]
\[ \Rightarrow \] \(\frac{{AN}}{{AD}} = \frac{{AO}}{{AC}}\)
Xét \[\Delta \]ANO và \[\Delta \]ADC: \(\left\{ {\begin{array}{*{20}{c}}{\frac{{AN}}{{AD}} = \frac{{AO}}{{AC}}}\\{\hat A\;chung}\end{array}} \right.\)
\[ \Rightarrow \]
\[ \Rightarrow \] \(\widehat {AON} = \widehat {ACD} = 90^\circ \)
Chứng minh tương tự \(\widehat {AOM} = \widehat {ABD} = 90^\circ \)
\( \Rightarrow \widehat {AOM} + \widehat {AON} = 90^\circ + 90^\circ = 180^\circ \)
Hay \[\widehat {AMN} = 180^\circ \]\[ \Rightarrow A,\,M,\,N\] thẳng hàng .
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số bảng đấu dự kiến ban đầu là x (bảng) \(\left( {x \in N*;\,x > 3} \right)\).
Số đội mỗi bảng ban đầu là \(\frac{{56}}{x}\)(đội)
Số đội tham dự thực tế là \(56 - 1 = 55\)(đội)
Tổng số bảng đấu giảm đi 3 bảng nên số bảng lúc sau là \(x - 3\)(bảng)
Số đội mỗi bảng lúc sau là \(\frac{{55}}{{x - 3}}\)(đội)
Vì tăng thêm mỗi bảng 1 đội nên ta có phương trình:\(\frac{{55}}{{x - 3}} - \frac{{56}}{x} = 1\)
\( \Rightarrow \frac{{ - x + 168}}{{x\left( {x - 3} \right)}} = 1 \Rightarrow {x^2} - 2x - 168 = 0\)
Giải phương trình tim được 2 nghiệm x1 = 14 (tm) hoặc x2 = -12 ( loại)
Vậy số bảng dự kiến ban đầu là 14 bảng đấu.
Lời giải
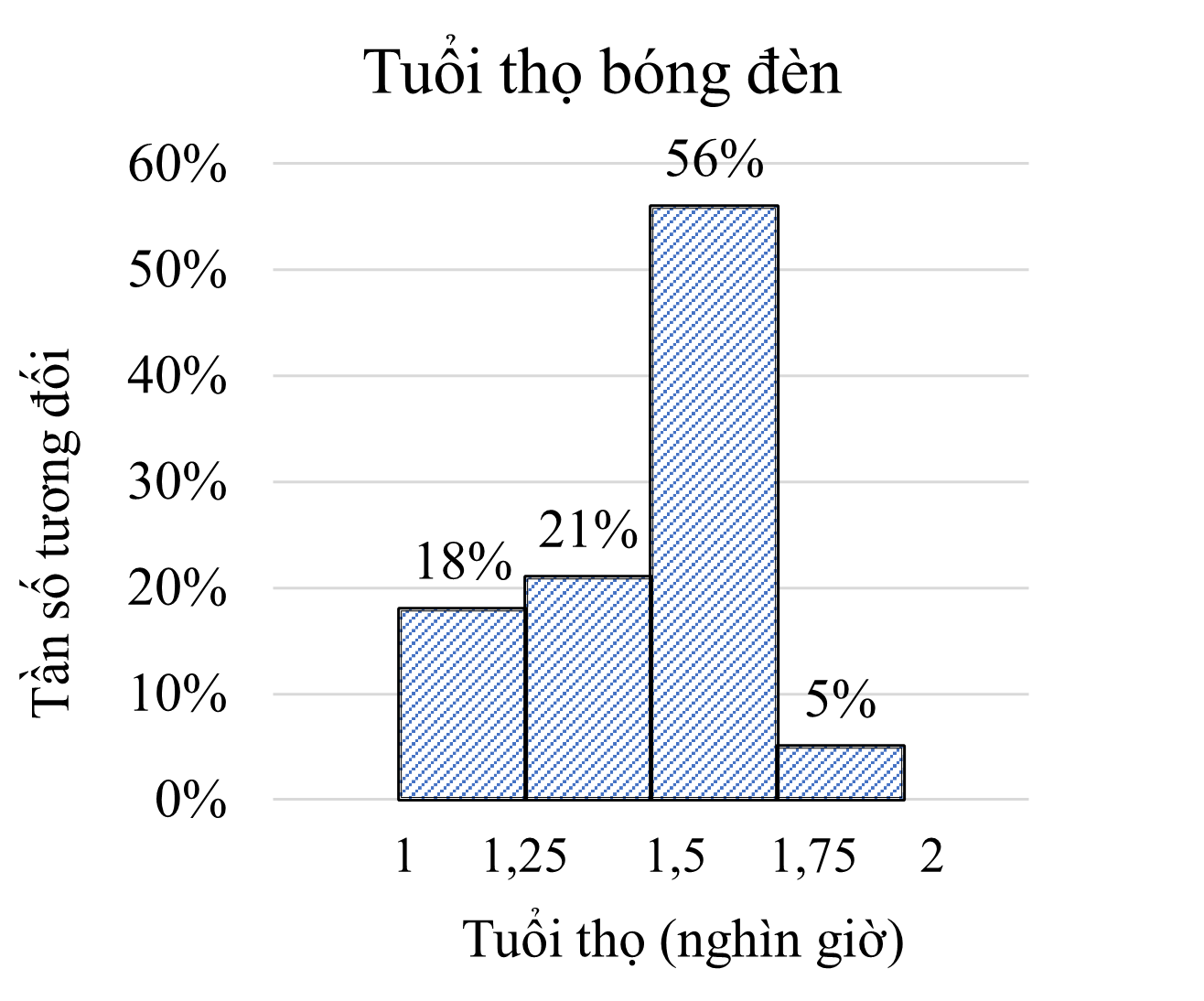
Tần số \[5\% \] là tần số tương đối của nhóm \[\left[ {1\,,75;2} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.