Trong mặt phẳng tọa độ \(Oxy\) cho parabol \(\left( P \right):y = 2{x^2}\) và đường thẳng \(\left( d \right):\,\,y = - 2x + 4.\)
a. Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng mặt phẳng tọa độ.
b. Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.
Trong mặt phẳng tọa độ \(Oxy\) cho parabol \(\left( P \right):y = 2{x^2}\) và đường thẳng \(\left( d \right):\,\,y = - 2x + 4.\)
a. Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng mặt phẳng tọa độ.
b. Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.
Quảng cáo
Trả lời:
Trong mặt phẳng tọa độ Oxy cho parabol \(\left( P \right):y = 2{x^2}\) và đường thẳng \(\left( d \right):y = - 2x + 4.\)
a.Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng mặt phẳng tọa độ.
.Trên cùng hệ trục tọa độ, vẽ parabol \((P)\) và đường thẳng \((d)\).
\(x\).\( - 1\).\(0\).\(1\)
\(y = 2{x^2}\).\(2\) .\(0\).\(2\)
.\(x\).\(0\).\(2\)
\(y = - 2x + 4\).\(4\) .\(0\)
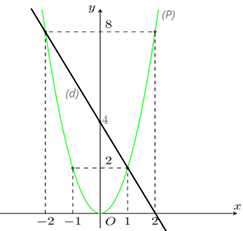
b.Tìm tọa độ giao điểm của \(\left( P \right):y = 2{x^2}\) và \(\left( d \right):y = - 2x + 4\) bằng phép tính.
.Phương trình hoành độ giao điểm của \[\left( P \right)\] và \[\left( d \right)\]: \[2{x^2} = - 2x + 4\]
\[ \Leftrightarrow 2{x^2} + 2x - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = 8\\x = 1\,\,\,\,\, \Rightarrow y = 2\end{array} \right..\]
Vậy tọa độ giao điểm của \((P)\) và \((d)\) là \[\left( { - 2;\,\,8} \right)\]và \[\left( {1;\,\,2} \right).\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
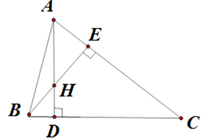
a. Chứng minh tứ giác \(CDHE\;\) nội tiếp đường tròn.
Xét \(\Delta \;ABC\) có:
\(AD\;\)là đường cao \[ \Rightarrow \]\(\widehat {ADC} = {90^0}\) \[ \Rightarrow \]\({\rm{\;\;}}\widehat {HDC} = {90^0}.\)
\(BE\;\)là đường cao \[ \Rightarrow \]\(\widehat {BEC} = {90^0}\)\[ \Rightarrow \]\({\rm{\;\;}}\widehat {HEC} = {90^0}.\)
Xét tứ giác \(CDHE\) có: \(\widehat {HDC} + \widehat {HEC} = {90^0} + {90^0} = {180^0}.\)
Vậy tứ giác \(CDHE\) là tứ giác nội tiếp đường tròn.
b. Chứng minh: \(HA.\;HD = HB.\;HE.\)
Xét \(\Delta \;AHE\;\)và \(\Delta BHD\) có:
\(\widehat {BHD} = \widehat {AHE}\) ( đối đỉnh)
\(\widehat D = \widehat E = {90^0}.\)
\(\Delta \;BHD\;\)và \(\;\Delta \;AHE\) đồng dạng \(\left( {\;g\'o c - g\'o c} \right)\)
Vậy \(\;\;\frac{{BH}}{{HA}} = {\rm{\;}}\frac{{HD}}{{HE}}\) \[ \Leftrightarrow \]\(BH.\;HE = HD.\;HA\) (đpcm)
c. Gọi điểm \(\;I\) là tâm đường tròn ngoại tiếp tứ giác \(CDHE.\) Chứng minh \(IE\) là tiếp tuyến của đường tròn đường kính \(AB.\) .
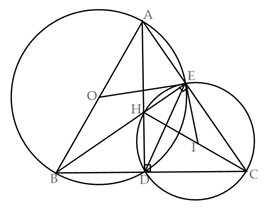
* Xét tứ giác \(BAED\) có: \(\widehat {BDA} = \widehat {BEA} = {90^0}\)\[ \Rightarrow \]Tứ giác \(BAED\;\) nội tiếp đường tròn có tâm \(O,\) đường kính\(AB\)\[ \Rightarrow \]\(\widehat {OEA} = \widehat {OAE}\) (vì \(\Delta OAE\) cân tại \(O)\) (1)
\[ \Rightarrow \] \(\widehat {BAE} = \widehat {EDC}\) ( cùng bù với \(\widehat {EDB}\)) hay \(\widehat {OAE} = \widehat {EDC}\) (2)
* Xét đường tròn \(\left( I \right)\) có: \(\widehat {EDC} = \widehat {EHC} = \;\frac{1}{2}\)sđ (3)
* Ta có \(\Delta IEH\) cân tại \(I\)\[ \Rightarrow \]\(\widehat {EHI} = \widehat {IEH}\) hay \(\widehat {EHC} = \widehat {IEB}\) (4)
Từ (1), (2), (3), (4) \[ \Rightarrow \]\(\widehat {OEA} = \widehat {IEB}\)
Mà \(\widehat {OEI} = \widehat {OEB} + \widehat {IEB}\)\( = \widehat {OEB} + \widehat {OEA} = {90^0}\)
Vậy \[OE \bot EI\] tại \(E\) \[ \Rightarrow \]\(EI\) là tiếp tuyến của đường tròn đường kính \(AB.\)
Lời giải
a. Giải phương trình \(3{x^2} - 7x + 4 = 0.\)
Ta có \[a + b + c = 3 + ( - 7) + 4 = 0\]
Vậy phương trình có hai nghiệm phân biệt \({x_1} = 1\) và \({x_2} = \frac{4}{3}.\)
b. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{3x + y = 9}\\{2x - y = 1}\end{array}} \right..\)
\[ \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\2x - y = 1\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2.2 - y = 1\end{array} \right.\] \[ \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right..\]
Vậy hệ phương trình có nghiệm duy nhất \[\left( {2;3} \right).\]
c. Cho phương trình \({x^2} - 2x + m + 3 = 0\;\;\)(\(x\) là ẩn số, \(m\) là tham số). Với giá trị nào của \(m\) thì phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(\;x_1^2.{x_2} + {x_1}.x_2^2 = - \,4.\)
Ta có: \[\Delta = - 8 - 4m\]
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi \(\Delta \; > 0\)
\[ \Leftrightarrow m < - 2.\]
Theo hệ thức Vi-ét \[\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}.{x_2} = m + 3\end{array} \right.\]
Theo đề bài \(x_1^2.{x_2} + {x_1}.x_2^2 = - 4\)
\[ \Leftrightarrow \]\({\rm{\;}}{x_1}.{x_2}.\left( {{x_1} + {x_2}} \right) = - 4{\rm{\;}} \Leftrightarrow \left( {m + 3} \right).2 = - 4{\rm{\;}}\)
\[ \Leftrightarrow \]\(m = - 5\) (thỏa mãn).
Vậy \(m = - 5{\rm{\;}}\)thì phương trình có hai nghiệm phân biệt thỏa mãn \(x_1^2.{x_2} + {x_1}.x_2^2 = - 4.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.