a. Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(\;AH = 3\;cm,\;\)\(HC = 4\;cm.\) Tính độ dài đoạn thẳng \(HB,\;\,AC\;\)và số đo góc \(C\)(kết quả làm tròn đến độ).
b. Để xác định chiều cao của một tòa tháp cao tầng (hình vẽ bên), một người đứng tại điểm \(C\) cách chân tháp một khoảng \(CD = 60\,m,\) sử dụng giác kế nhìn thấy đỉnh tòa tháp với góc \(\widehat {AOB} = {60^0}.\) Hãy tính chiều cao của tòa tháp. Biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế là \(OC = 1\,m,\) (kết quả làm tròn đến hàng đơn vị).
a. Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(\;AH = 3\;cm,\;\)\(HC = 4\;cm.\) Tính độ dài đoạn thẳng \(HB,\;\,AC\;\)và số đo góc \(C\)(kết quả làm tròn đến độ).
b. Để xác định chiều cao của một tòa tháp cao tầng (hình vẽ bên), một người đứng tại điểm \(C\) cách chân tháp một khoảng \(CD = 60\,m,\) sử dụng giác kế nhìn thấy đỉnh tòa tháp với góc \(\widehat {AOB} = {60^0}.\) Hãy tính chiều cao của tòa tháp. Biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế là \(OC = 1\,m,\) (kết quả làm tròn đến hàng đơn vị).
Quảng cáo
Trả lời:
a. Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH\;.\) Biết \(\;AH = 3\;cm,\,\,\;HC = 4\;cm.\) Tính độ dài đoạn thẳng \(HB,\;\;AC\;\)và số đo góc \(C\)(kết quả làm tròn đến độ).
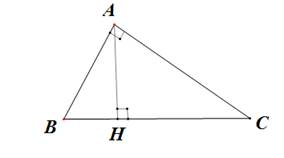
* Xét tam giác \(ABC\)vuông tại \(A\) nên \(A{H^2} = HB.HC\)
\[ \Rightarrow \]\(HB = \frac{{A{H^2}}}{{HC}} = \;\frac{9}{4} = 2,25\;cm.\).
* Xét tam giác vuông \(AHC\) có:
\(A{C^2} = A{H^2} + H{C^2}\) (định lí pytago)
\[ \Rightarrow \]\(AC = \;\sqrt {{3^2} + {4^2}} \)\( = 5\,\,cm.\).
* \(\cos C = \frac{{CH}}{{CA}} = 0,8\) hoặc \(\cos C = \frac{{CH}}{{CA}} = \frac{4}{5}\).
Vậy \(\widehat C \approx {37^0}.\).
b. Để xác định chiều cao của một tòa tháp cao tầng (hình vẽ bên), một người đứng tại điểm \(C\)cách chân tháp một khoảng \(CD = 60\,m,\) sử dụng giác kế nhìn thấy đỉnh tòa tháp với góc \(\widehat {AOB} = {60^0}.\) Hãy Tính chiều cao của tòa tháp. Biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế là \(OC = 1\,m,\) (kết quả làm tròn đến hàng đơn vị).
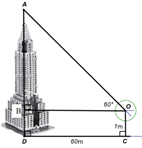
Tam giác \[OAB\] vuông tại \[B,\] có \(AB = 60.\tan {60^0}.\) .
Vậy chiều cao của ngọn tháp là \(h \approx 105\,\,m.\) .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
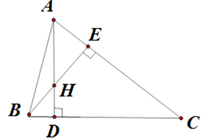
a. Chứng minh tứ giác \(CDHE\;\) nội tiếp đường tròn.
Xét \(\Delta \;ABC\) có:
\(AD\;\)là đường cao \[ \Rightarrow \]\(\widehat {ADC} = {90^0}\) \[ \Rightarrow \]\({\rm{\;\;}}\widehat {HDC} = {90^0}.\)
\(BE\;\)là đường cao \[ \Rightarrow \]\(\widehat {BEC} = {90^0}\)\[ \Rightarrow \]\({\rm{\;\;}}\widehat {HEC} = {90^0}.\)
Xét tứ giác \(CDHE\) có: \(\widehat {HDC} + \widehat {HEC} = {90^0} + {90^0} = {180^0}.\)
Vậy tứ giác \(CDHE\) là tứ giác nội tiếp đường tròn.
b. Chứng minh: \(HA.\;HD = HB.\;HE.\)
Xét \(\Delta \;AHE\;\)và \(\Delta BHD\) có:
\(\widehat {BHD} = \widehat {AHE}\) ( đối đỉnh)
\(\widehat D = \widehat E = {90^0}.\)
\(\Delta \;BHD\;\)và \(\;\Delta \;AHE\) đồng dạng \(\left( {\;g\'o c - g\'o c} \right)\)
Vậy \(\;\;\frac{{BH}}{{HA}} = {\rm{\;}}\frac{{HD}}{{HE}}\) \[ \Leftrightarrow \]\(BH.\;HE = HD.\;HA\) (đpcm)
c. Gọi điểm \(\;I\) là tâm đường tròn ngoại tiếp tứ giác \(CDHE.\) Chứng minh \(IE\) là tiếp tuyến của đường tròn đường kính \(AB.\) .
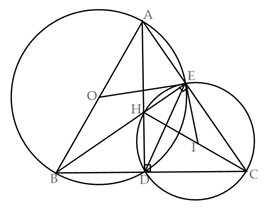
* Xét tứ giác \(BAED\) có: \(\widehat {BDA} = \widehat {BEA} = {90^0}\)\[ \Rightarrow \]Tứ giác \(BAED\;\) nội tiếp đường tròn có tâm \(O,\) đường kính\(AB\)\[ \Rightarrow \]\(\widehat {OEA} = \widehat {OAE}\) (vì \(\Delta OAE\) cân tại \(O)\) (1)
\[ \Rightarrow \] \(\widehat {BAE} = \widehat {EDC}\) ( cùng bù với \(\widehat {EDB}\)) hay \(\widehat {OAE} = \widehat {EDC}\) (2)
* Xét đường tròn \(\left( I \right)\) có: \(\widehat {EDC} = \widehat {EHC} = \;\frac{1}{2}\)sđ (3)
* Ta có \(\Delta IEH\) cân tại \(I\)\[ \Rightarrow \]\(\widehat {EHI} = \widehat {IEH}\) hay \(\widehat {EHC} = \widehat {IEB}\) (4)
Từ (1), (2), (3), (4) \[ \Rightarrow \]\(\widehat {OEA} = \widehat {IEB}\)
Mà \(\widehat {OEI} = \widehat {OEB} + \widehat {IEB}\)\( = \widehat {OEB} + \widehat {OEA} = {90^0}\)
Vậy \[OE \bot EI\] tại \(E\) \[ \Rightarrow \]\(EI\) là tiếp tuyến của đường tròn đường kính \(AB.\)
Lời giải
a. Giải phương trình \(3{x^2} - 7x + 4 = 0.\)
Ta có \[a + b + c = 3 + ( - 7) + 4 = 0\]
Vậy phương trình có hai nghiệm phân biệt \({x_1} = 1\) và \({x_2} = \frac{4}{3}.\)
b. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{3x + y = 9}\\{2x - y = 1}\end{array}} \right..\)
\[ \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\2x - y = 1\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2.2 - y = 1\end{array} \right.\] \[ \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right..\]
Vậy hệ phương trình có nghiệm duy nhất \[\left( {2;3} \right).\]
c. Cho phương trình \({x^2} - 2x + m + 3 = 0\;\;\)(\(x\) là ẩn số, \(m\) là tham số). Với giá trị nào của \(m\) thì phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(\;x_1^2.{x_2} + {x_1}.x_2^2 = - \,4.\)
Ta có: \[\Delta = - 8 - 4m\]
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi \(\Delta \; > 0\)
\[ \Leftrightarrow m < - 2.\]
Theo hệ thức Vi-ét \[\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}.{x_2} = m + 3\end{array} \right.\]
Theo đề bài \(x_1^2.{x_2} + {x_1}.x_2^2 = - 4\)
\[ \Leftrightarrow \]\({\rm{\;}}{x_1}.{x_2}.\left( {{x_1} + {x_2}} \right) = - 4{\rm{\;}} \Leftrightarrow \left( {m + 3} \right).2 = - 4{\rm{\;}}\)
\[ \Leftrightarrow \]\(m = - 5\) (thỏa mãn).
Vậy \(m = - 5{\rm{\;}}\)thì phương trình có hai nghiệm phân biệt thỏa mãn \(x_1^2.{x_2} + {x_1}.x_2^2 = - 4.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.