a) Chứng minh đẳng thức \[\sqrt {27}  - 2\sqrt {12}  + \sqrt {4 - 2\sqrt 3 }  =  - 1.\]

b) Rút gọn biểu thức \[A = \left( {\frac{{9 - \sqrt x }}{{x - 9}} + \frac{2}{{\sqrt x  + 3}}} \right):\frac{{\sqrt x  + 1}}{{\sqrt x  - 3}}\]  với \(x \ge 0\)và \(x \ne 9.\)

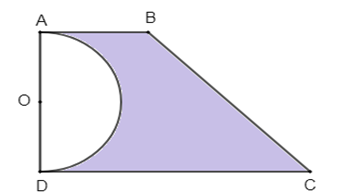
1)Diện tích hình thang \[ABCD\] là \[\frac{{\left( {AB + DC} \right).AD}}{2} = \frac{{\left( {3 + 7} \right).5}}{2} = 25\,{m^2}.\]

Diện tích nửa hình tròn đường kính \[AD\] là \[\frac{{\pi .{{\left( {2,5} \right)}^2}}}{2} = \frac{{25\pi }}{8}\,{m^2}.\]

Diện tích phần đất trồng cỏ là \[25 - \frac{{25\pi }}{8} \approx 15,19\,{m^2}.\]

                  Chú ý: Nếu học sinh không làm tròn thì trừ 0,25 điểm bước này.

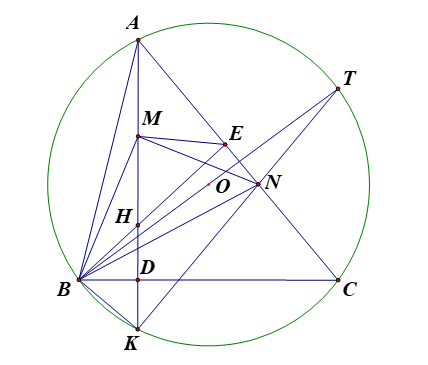
2a) Ta có \[\widehat {BMN} = {90^0} \Rightarrow \] \[M\]thuộc đường tròn đường kính \[BN.\]

Ta có \[\widehat {BEN} = {90^0} \Rightarrow \] \[E\] thuộc đường tròn đường kính \[BN.\]

Do đó bốn điểm \[B,\,M,\,E,\,N\] cùng thuộc đường tròn đường kính \[BN.\]

Chứng minh được \[\widehat {MBN} = \widehat {MEA}\].

Xét \[\Delta AEH\] vuông tại \[E,\] có \[EM\] là đường trung tuyến

\[ \Rightarrow EM = AM \Rightarrow \Delta AME\] cân tại \[M \Rightarrow \widehat {MEA} = \widehat {MAE} \Rightarrow \widehat {MBN} = \widehat {KAC}.\]

b)Xét \[(O)\]có \[\widehat {KBC} = \widehat {KAC}\] mà \[\widehat {KAC} = \widehat {EBC}\] (cùng phụ với \[\widehat {ACB}\]) \[ \Rightarrow \widehat {KBC} = \widehat {EBC}\]

\[ \Rightarrow BC\] là tia phân giác của góc \[\widehat {KBH}.\] Lại có \[BC \bot HK \Rightarrow \Delta BHK\]cân tại \[B.\]

\[ \Rightarrow \widehat {BKH} = \widehat {BHK}.\] Ta có \[\widehat {BHK} = \widehat {MHE} = \widehat {MEH} = \widehat {MNB} \Rightarrow \widehat {BKM} = \widehat {BNM.}\]

Do đó tứ giác \[BMNK\] nội tiếp.

\[ \Rightarrow \widehat {BMN} + \widehat {BKN} = {180^0} \Rightarrow \widehat {BKN} = \widehat {BKT} = {90^0}\]\[ \Rightarrow K\]thuộc đường tròn đường kính \[BT.\] Mà \[B,\,K,\,T \in \left( O \right) \Rightarrow BT\]là đường kính của \[(O) \Rightarrow B,\,O,\,T\]thẳng hàng.

ĐKXĐ: \(x \ne 4;\,y \ne 0\)

PT\(\left( 1 \right) \Leftrightarrow x - 4 =  - 3y\)

Thay \(x - 4 =  - 3y\) vào PT\(\left( 2 \right)\) ta có \(\frac{1}{{ - 3y}} + \frac{1}{y} = 1 \Leftrightarrow y = \frac{2}{3} \Rightarrow x = 2.\)

Đối chiếu với ĐKXĐ ta có \(\left( {x;y} \right) = \left( {2;\frac{2}{3}} \right)\) là nghiệm của hệ.