(0,5 điểm) Một cửa hàng xăng dầu cần xây một bồn chứa dầu hình trụ bằng thép có thể tích \(54\pi \left( {{m^3}} \right)\) và giá mỗi mét vuông thép là 500 ngàn đồng. Hỏi số tiền thấp nhất mà cửa hàng phải trả ? ( kết quả làm tròn đến hàng đơn vị)
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 45 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi bán kính đáy là \(x\,(\;m)\,(x > 0)\), chiều cao bồn chứa là \(h\,(\;m)\).
Thể tích chứa của bồn là \(V = \pi {x^2} \cdot h = 54\pi \Rightarrow h = \frac{{54}}{{{x^2}}}\)(\[m\]).
Diện tích toàn phần của bồn chứa là: \({S_{TP}} = 2\pi {x^2} + 2\pi x \cdot h = 2\pi {x^2} + \frac{{108\pi }}{x}\left( {\;{m^2}} \right)\)
Để chi phí xây dựng thấp nhất thì diện tích toàn phần của bồn phải nhỏ nhất.
Ta có
\({S_{TP}} = 2\pi {x^2} + \frac{{108\pi }}{x} = 2\pi {x^2} + \frac{{54\pi }}{x} + \frac{{54\pi }}{x} \ge 3\sqrt[3]{{2\pi {x^2}.\frac{{54\pi }}{x}.\frac{{54\pi }}{x}}} = 54\pi \)( BĐT Cô si cho 3 số không âm)
\({S_{TP}}\) đạt giá trị nhỏ nhất bằng \(54\pi \left( {{m^2}} \right)\) khi \(2\pi {x^2} = \frac{{54\pi }}{x} \Rightarrow {x^3} = 27 \Rightarrow x = 3\) (m)
Khi đó số tiền xây bồn thấp nhất mà cửa hàng phải trả là : \(54\pi .500000 \approx \) 84 823 002 (đồng)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi số tiền bác Tuấn đã vay ngân hàng Sacombank và Vietcombank lần lượt là \[x,\]\[y\](tỉ đồng)
Điều kiện: \[0 < x < 5;\,\]\[0 < y < 5.\]
Theo bài, tổng số tiền vay là 5 tỉ đồng nên ta có phương trình:\[x + y = 5\].
Số tiền lãi phải trả mỗi năm cho ngân hàng Sacombank là \[x.12\% = 0,12x\](tỉ đồng).
Số tiền lãi phải trả mỗi năm cho ngân hàng Vietcombank là \[y.11\% = 0,11y\](tỉ đồng).
Theo bài, tổng số tiền lãi phải trả là 570 triệu đồng nên ta có phương trình:
\[0,12x + 0,11y = 0,57\]hay \[12x + 11y = 57.\]
Ta có hệ phương trình: \[\left\{ {\begin{array}{*{20}{l}}{x + y = 5}\\{12x + 11y = 57.}\end{array}} \right.\].
Nhân hai vế của phương trình thứ nhất với 11, ta được hệ phương trình: \[\left\{ {\begin{array}{*{20}{l}}{11x + 11y = 55}\\{12x + 11y = 57}\end{array}} \right.\].
Trừ hai vế của hai phương trình trên, ta được: \[x = 2\].
Thay \[x = 2\] vào phương trình \[x + y = 5\] ,
Ta được \[2 + y = 5\].
\[y = 3.\]
Ta thấy \[x = 2\] và \[y = 3.\] thỏa mãn điều kiện.
Vậy số tiền bác Tuấn đã vay của ngân hàng Sacombank là 2 tỉ đồng và Vietcombank là 3 tỉ đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
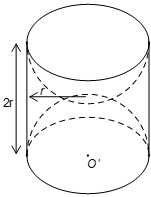
a. Thể tích của khối gỗ lúc chưa khoét là:
\(V = \pi {r^2}h = \pi {.10^2}.20 \approx 6283\left( {c{m^3}} \right)\)
b. Diện tích bề mặt của khối gỗ còn lại gồm diện tích xung quanh của hình trụ (có bán kính đáy là \[r = 10\left( {cm} \right),\]và chiều cao \[h = 20(cm)\]) và diện tích hai nửa mặt cầu bán kính \[r = 10\left( {cm} \right),\]
Diện tích cần tìm là: \[S = 2\pi r.h + 4\pi {r^2} = 2\pi .10.20 + 4.\pi {.10^2} \approx 2513\left( {c{m^2}} \right)\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập