(2,5 điểm)
Bác Tuấn vay tổng số tiền là 5 tỉ đồng từ hai ngân hàng Sacombank và Vietcombank đầu tư vào bất động sản. Sau một năm, tổng số tiền lãi phải trả cho hai ngân hàng trên là 570 triệu đồng. Lãi suất cho vay của ngân hàng Sacombank là 12% /năm và của Vietcombank là 11% /năm. Tính số tiền bác Tuấn đã vay của mỗi ngân hàng.
(2,5 điểm)
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 45 !!
Quảng cáo
Trả lời:
Gọi số tiền bác Tuấn đã vay ngân hàng Sacombank và Vietcombank lần lượt là \[x,\]\[y\](tỉ đồng)
Điều kiện: \[0 < x < 5;\,\]\[0 < y < 5.\]
Theo bài, tổng số tiền vay là 5 tỉ đồng nên ta có phương trình:\[x + y = 5\].
Số tiền lãi phải trả mỗi năm cho ngân hàng Sacombank là \[x.12\% = 0,12x\](tỉ đồng).
Số tiền lãi phải trả mỗi năm cho ngân hàng Vietcombank là \[y.11\% = 0,11y\](tỉ đồng).
Theo bài, tổng số tiền lãi phải trả là 570 triệu đồng nên ta có phương trình:
\[0,12x + 0,11y = 0,57\]hay \[12x + 11y = 57.\]
Ta có hệ phương trình: \[\left\{ {\begin{array}{*{20}{l}}{x + y = 5}\\{12x + 11y = 57.}\end{array}} \right.\].
Nhân hai vế của phương trình thứ nhất với 11, ta được hệ phương trình: \[\left\{ {\begin{array}{*{20}{l}}{11x + 11y = 55}\\{12x + 11y = 57}\end{array}} \right.\].
Trừ hai vế của hai phương trình trên, ta được: \[x = 2\].
Thay \[x = 2\] vào phương trình \[x + y = 5\] ,
Ta được \[2 + y = 5\].
\[y = 3.\]
Ta thấy \[x = 2\] và \[y = 3.\] thỏa mãn điều kiện.
Vậy số tiền bác Tuấn đã vay của ngân hàng Sacombank là 2 tỉ đồng và Vietcombank là 3 tỉ đồng.
Câu hỏi cùng đoạn
Câu 2:
Một công nhân dự định làm 72 sản phẩm trong một thời gian đã định. Nhưng thực tế xí nghiệp lại giao 80 sản phẩm. Mặc dù người đó mỗi giờ đã làm thêm một sản phẩm so với dự kiến, nhưng thời gian hoàn thành công việc vẫn chậm so với dự định là 12 phút. Tính số sản phẩm dự kiến làm trong 1 giờ của người đó. Biết mỗi giờ người đó làm không quá 20 sản phẩm.(Giả định rằng số sản phẩm mà công nhân đó làm được trong mỗi giờ là bằng nhau).
Gọi số sản phẩm dự định làm trong 1 giờ của người đó là \(x\,\)\(\left( {x \in {\mathbb{N}^*},\,x < 20} \right)\)
Theo dự định: Thời gian hoàn thành là \(\frac{{72}}{x}\) (ngày)
Thực tế: Mỗi giờ người đó đã làm \(x + 1\) ( sản phẩm)
Thời gian hoàn thành \(\frac{{80}}{{x + 1}}\) (ngày).
Vì thời gian hoàn thành công việc vẫn chậm hơn so với dự định 12 phút \( = \frac{1}{5}h\)
Nên ta có phương trình:
\(\frac{{80}}{{x + 1}} - \frac{{72}}{x} = \frac{1}{5}{\rm{ }}\)
\(\frac{{400x - 360(x + 1)}}{{5x(x + 1)}} = \frac{{x(x + 1)}}{{5x(x + 1)}}\)
\(40x - 360 = {x^2} + x\)
\({x^2} - 39x + 360 = 0\)
\(\Delta = {39^2} - 4.360 = 81 > 0 \Rightarrow \sqrt \Delta = 9\)
Phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - ( - 39) + 9}}{2} = 24\) (loại) và \({x_2} = \frac{{ - ( - 39) - 9}}{2} = 15\) (tmđk).
Vậy số sản phẩm dự định làm trong 1 giờ của người đó là 15 sản phẩm.Câu 3:
a). Hãy tìm một phương trình bậc hai \[a{x^2} + bx + c = 0\] với các hệ số \[a,b,c\] là số nguyên nhận \(x = \frac{{\sqrt 5 - 2}}{3}\) làm nghiệm.
b). Tính tổng lập phương hai nghiệm của phương trình vừa tìm được ở câu a)
a). Ta có \(x = \frac{{\sqrt 5 - 2}}{3}\)
\(3x = \sqrt 5 - 2\)
\(3x + 2 = \sqrt 5 \)
\({\left( {3x + 2} \right)^2} = 5\)
\(9{x^2} + 12x + 4 = 5\)
\(9{x^2} + 12x - 1 = 0\)
Vậy phương trình bậc hai cần tìm là: \(9{x^2} + 12x - 1 = 0\)
b). Theo hệ thức Vi-ét, ta có: \[\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - 4}}{3}\\{x_1}.{x_2} = \frac{{ - 1}}{9}\end{array} \right.\]
Ta có \[x_1^3 + x_2^3 = {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}.{x_2}\left( {{x_1} + {x_2}} \right) = {\left( {\frac{{ - 4}}{3}} \right)^3} - 3\left( {\frac{{ - 1}}{9}} \right)\left( {\frac{{ - 4}}{3}} \right) = \frac{{ - 76}}{{27}}\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
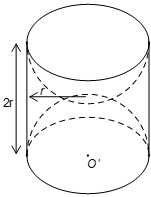
a. Thể tích của khối gỗ lúc chưa khoét là:
\(V = \pi {r^2}h = \pi {.10^2}.20 \approx 6283\left( {c{m^3}} \right)\)
b. Diện tích bề mặt của khối gỗ còn lại gồm diện tích xung quanh của hình trụ (có bán kính đáy là \[r = 10\left( {cm} \right),\]và chiều cao \[h = 20(cm)\]) và diện tích hai nửa mặt cầu bán kính \[r = 10\left( {cm} \right),\]
Diện tích cần tìm là: \[S = 2\pi r.h + 4\pi {r^2} = 2\pi .10.20 + 4.\pi {.10^2} \approx 2513\left( {c{m^2}} \right)\]
Lời giải
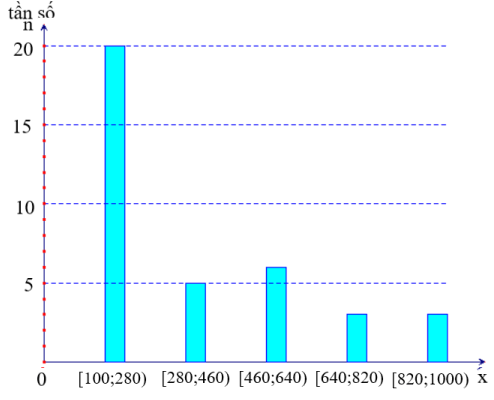
a) Tần số ghép nhóm của nhóm \[{\rm{[}}460;640)\]là 6.
b .Tần số tương đối ghép nhóm của nhóm \[{\rm{[10}}0;280)\]là \[f = \frac{{20}}{{37}}.100\% \approx 54\% \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.