Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{x + d}}\) có đồ thị như hình vẽ dưới đây. Biết rằng điểm \(O\left( {0;0} \right)\) là điểm cực đại của đồ thị hàm số.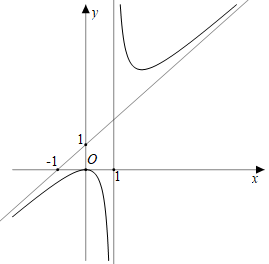
Quảng cáo
Trả lời:
a) Phương trình đường tiệm cận xiên của đồ thị hàm số là \(y = ax + b\left( d \right)\).
Tiệm cận xiên của đồ thị hàm số đi qua điểm \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\).
Thay vào \(\left( d \right)\) ta có \(\left\{ {\begin{array}{*{20}{c}}{ - a + b = 0}\\{b = 1}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = 1}\end{array}} \right.} \right.\).
Vậy tiệm cận xiên của đồ thị hàm số là \(y = x + 1\). Nên a đúng.
b) Do đồ thị hàm số qua điểm \(O\left( {0;0} \right)\) nên thay vào hàm số ta được \(\frac{c}{d} = 0 \Rightarrow c = 0\).
Đồ thị hàm số có tiệm cận đứng là \(x = 1\)\( \Rightarrow d = - 1\).
Khi đó \(y = f\left( x \right) = \frac{{a{x^2} + bx}}{{x - 1}} = ax + a + b + \frac{{a + b}}{{x - 1}}\).
Do tiệm cận xiên \(y = x + 1\) nên \(\left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = 0}\end{array}} \right.\).
Vậy \(y = f\left( x \right) = x + 1 + \frac{1}{{x - 1}}\)
\[ \Rightarrow y' = 1 - \frac{1}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{{\left( {x - 1} \right)}^2} - 1}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Rightarrow {\left( {x - 1} \right)^2} - 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\]
Mà điểm \(O\left( {0;0} \right)\) là điểm cực đại của đồ thị hàm số.
Vì thế tọa độ điểm cực tiểu là \(T\left( {2;4} \right)\). Nên b đúng.
c) Trên khoảng \(\left( {1; + \infty } \right)\) đồ thị hàm số vừa đi lên, vừa đi xuống nên hàm số vừa đồng biến, vừa nghịch biến trên \(\left( {1; + \infty } \right)\). Nên c sai.
d) Tiếp tuyến của đồ thị hàm số tại \(A\left( {{x_A};{x_A} + 1 + \frac{1}{{{x_A} - 1}}} \right)\), \(B\left( {{x_B};{x_B} + 1 + \frac{1}{{{x_B} - 1}}} \right)\) (\({x_A} \ne {x_B}\)) thuộc đồ thị song song với nhau nên
\[{y'_{\left( A \right)}} = {y'_{\left( B \right)}} \Rightarrow 1 - \frac{1}{{{{\left( {{x_A} - 1} \right)}^2}}} = 1 - \frac{1}{{{{\left( {{x_B} - 1} \right)}^2}}}\]
\[ \Rightarrow {\left( {{x_A} - 1} \right)^2} = {\left( {{x_B} - 1} \right)^2}\]\[ \Rightarrow \left[ {\begin{array}{*{20}{c}}{{x_A} - 1 = {x_B} - 1}\\{{x_A} - 1 = - \left( {{x_B} - 1} \right)}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}}{{x_A} = {x_B}(loai)}\\{{x_A} + {x_B} = 2}\end{array}} \right.\].
Vậy: \[{x_A} + {x_B} = 2\], nên đặt \({x_A} = 1 - t,{x_B} = 1 + t\)
Vậy \(A\left( {1 - t;2 - t - \frac{1}{t}} \right)\), \(B\left( {1 + t;2 + t + \frac{1}{t}} \right)\).
\(\overrightarrow {AB} = \left( {2t;2t + \frac{2}{t}} \right)\). Véc tơ pháp tuyến của đường thẳng \(AB\) là \(\overrightarrow n = \left( {t + \frac{1}{t}; - t} \right)\) hay \(\overrightarrow {n'} = \left( {1 + \frac{1}{{{t^2}}}; - 1} \right)\).
Đặt \(s = 1 + \frac{1}{{{t^2}}}\).
Trung điểm của \(AB\) là \(I\left( {1;2} \right)\)
Vậy phương trình đường thẳng \(AB\) đi qua \(I\left( {1;2} \right)\) và có véc tơ pháp tuyến \(\overrightarrow {n'} = \left( {s; - 1} \right)\) là:
\(s\left( {x - 1} \right) - \left( {y - 2} \right) = 0\)\( \Leftrightarrow s.x - y + 2 - s = 0\).
\(d\left( {M;AB} \right) = \frac{{\left| {4s - 1 + 2 - s} \right|}}{{\sqrt {{s^2} + {1^2}} }} = \frac{{\left| {3s + 1} \right|}}{{\sqrt {{s^2} + 1} }} = \frac{{3s + 1}}{{\sqrt {{s^2} + 1} }}\left( {do\,s > 0} \right)\).
Đặt \(g\left( s \right) = \frac{{3s + 1}}{{\sqrt {{s^2} + 1} }}\)\( \Rightarrow g'\left( s \right) = \frac{{3 - s}}{{\sqrt {{{\left( {{s^2} + 1} \right)}^3}} }} = 0 \Rightarrow s = 3\).
Hàm \(g\left( x \right)\) đạt giá trị lớn nhất tại \(s = 3\). Khi đó \(s = 1 + \frac{1}{{{t^2}}} = 3 \Rightarrow {t^2} = \frac{1}{2}\).
\[\overrightarrow {AB} = \left( {2t;2t + \frac{2}{t}} \right)\]\[ \Rightarrow AB = \sqrt {{{\left( {2t} \right)}^2} + {{\left( {2t + \frac{2}{t}} \right)}^2}} = \sqrt {8{t^2} + 8 + \frac{4}{{{t^2}}}} \]
Thay \({t^2} = \frac{1}{2}\) vào \[AB = \sqrt {8.\frac{1}{2} + 8 + \frac{4}{{\frac{1}{2}}}} = \sqrt {20} = 2\sqrt 5 \]. Vậy d đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) Sai.
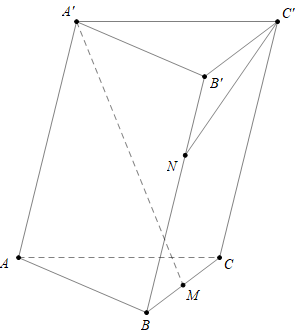
Ta có: \(\overrightarrow {A'M} = \frac{1}{2}\left( {\overrightarrow {A'B} + \overrightarrow {A'C} } \right)\)\( = \frac{1}{2}\left( {\overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'A} + \overrightarrow {A'C'} } \right) = \overrightarrow {A'A} + \frac{1}{2}\overrightarrow {A'B'} + \frac{1}{2}\overrightarrow {A'C'} \)\( = \frac{1}{2}.\overrightarrow {AB} + \frac{1}{2}.\overrightarrow {AC} - \overrightarrow {AA'} \). Suy ra \(x = y = \frac{1}{2};z = - 1 \Rightarrow x + y = - z\).
b) Đúng.
Ta có: \(\overrightarrow {BN} = \frac{2}{3}\overrightarrow {BB'} \Leftrightarrow \overrightarrow {BN} = \frac{2}{3}\left( {\overrightarrow {BN} + \overrightarrow {NB'} } \right) \Leftrightarrow \overrightarrow {BN} = 2\overrightarrow {NB'} \Leftrightarrow \overrightarrow {NB} = - 2\overrightarrow {NB'} \).
c) Đúng.
Ta có: \(\overrightarrow {AB} + \overrightarrow {CC'} = \overrightarrow {AB} + \overrightarrow {BB'} = \overrightarrow {AB'} \).
d) Đúng.
Ta có:\(\overrightarrow {C'N} = \overrightarrow {C'B'} + \overrightarrow {B'N} = \overrightarrow {A'B'} - \overrightarrow {A'C'} + \frac{1}{3}\overrightarrow {B'B} = \overrightarrow {AB} - \overrightarrow {AC} - \frac{1}{3}\overrightarrow {AA'} \)\( \Rightarrow \overrightarrow {A'M} .\overrightarrow {C'N} = \left( {\frac{1}{2}.\overrightarrow {AB} + \frac{1}{2}.\overrightarrow {AC} - \overrightarrow {AA'} } \right).\left( {\overrightarrow {AB} - \overrightarrow {AC} - \frac{1}{3}\overrightarrow {AA'} } \right)\)\( = \frac{1}{2}A{B^2} - \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AC} - \frac{1}{6}\overrightarrow {AB} .\overrightarrow {AA'} + \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AB} - \frac{1}{2}A{C^2} - \frac{1}{6}\overrightarrow {AC} .\overrightarrow {AA'} - \overrightarrow {AA'} .\overrightarrow {AB} + \overrightarrow {AA'} .\overrightarrow {AC} + \frac{1}{3}A{A'^2}\)
\( = \frac{1}{2}A{B^2} - \frac{1}{2}A{C^2} + \frac{1}{3}A{A'^2} - \frac{7}{6}\overrightarrow {AB} .\overrightarrow {AA'} + \frac{5}{6}\overrightarrow {AC} .\overrightarrow {AA'} \)
\( = = \frac{1}{2}{a^2} - \frac{1}{2}{a^2} + \frac{1}{3}{a^2} - \frac{7}{6}\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AA'} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AA'} } \right) + \frac{5}{6}\left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AA'} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {AA'} } \right)\)
\( = \frac{1}{3}{a^2} - \frac{7}{6}{a^2}.\cos \widehat {A'AB} + \frac{5}{6}{a^2}.\cos \widehat {A'AC} = \frac{1}{3}{a^2} - \frac{7}{6}{a^2}.\cos 120^\circ + \frac{5}{6}{a^2}.\cos 60^\circ \)
\( = \frac{4}{3}{a^2}\).
Lời giải
Đáp án: 1,65.
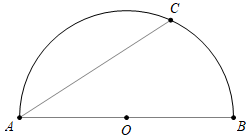
Đặt \(\widehat {CAB} = \varphi \left( {rad} \right)\), \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
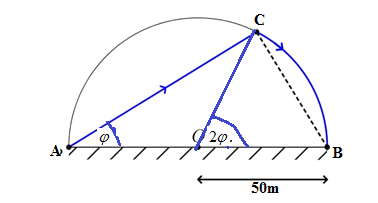
Ta có \(\Delta ABC\) vuông tại \(C\) \( \Rightarrow AC = AB.\cos \varphi = 0,1\cos \varphi \).
Mà \(\widehat {COR} = 2\widehat {CAB} = 2\varphi \).
Độ dài cung tròn .
Tổng thời gian người này di chuyển từ \(A\) đến \(C\) và đến B là: với \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
\( \Rightarrow t'\left( \varphi \right) = - \frac{1}{{50}}\sin \varphi + \frac{1}{{60}} = 0 \Leftrightarrow \sin \varphi = \frac{5}{6} \Rightarrow \varphi \approx 0,985\) rad.
Bảng biến thiên
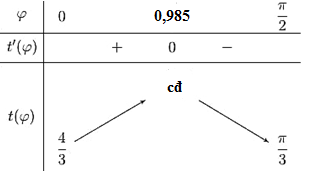
Vậy thời gian tối đa để di chuyển từ \(A\) đến \(C\)và đến B là \(t\left( {0,985} \right) = 0,027\)(giờ)\( \simeq 1,65\)phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.