Trong mặt phẳng tọa độ \(Oxy,\) cho đường tròn \(\left( C \right)\) tâm \(O\), bán kính bằng \(1\). Gọi \(T\) là tập hợp tất cả các điểm \(M\left( {x;y} \right)\), trong đó \(x,y \in \mathbb{Z}\), sao cho từ \(M\) kẻ được \(2\) tiếp tuyến \(MA\), \(MB\) đến \(\left( C \right)\) (\(A\), \(B\) là các tiếp điểm) thỏa mãn \(\widehat {AMB} \ge 60^\circ \). Chọn ngẫu nhiên \(2\) điểm trong \(T\). Biết xác suất để đường thẳng đi qua \(2\) điểm được chọn song song với trục \(Ox\) bằng \(\frac{1}{a}\). Tính \({a^2}\).
Trong mặt phẳng tọa độ \(Oxy,\) cho đường tròn \(\left( C \right)\) tâm \(O\), bán kính bằng \(1\). Gọi \(T\) là tập hợp tất cả các điểm \(M\left( {x;y} \right)\), trong đó \(x,y \in \mathbb{Z}\), sao cho từ \(M\) kẻ được \(2\) tiếp tuyến \(MA\), \(MB\) đến \(\left( C \right)\) (\(A\), \(B\) là các tiếp điểm) thỏa mãn \(\widehat {AMB} \ge 60^\circ \). Chọn ngẫu nhiên \(2\) điểm trong \(T\). Biết xác suất để đường thẳng đi qua \(2\) điểm được chọn song song với trục \(Ox\) bằng \(\frac{1}{a}\). Tính \({a^2}\).
Quảng cáo
Trả lời:
Đáp án:
Đáp án: 196.
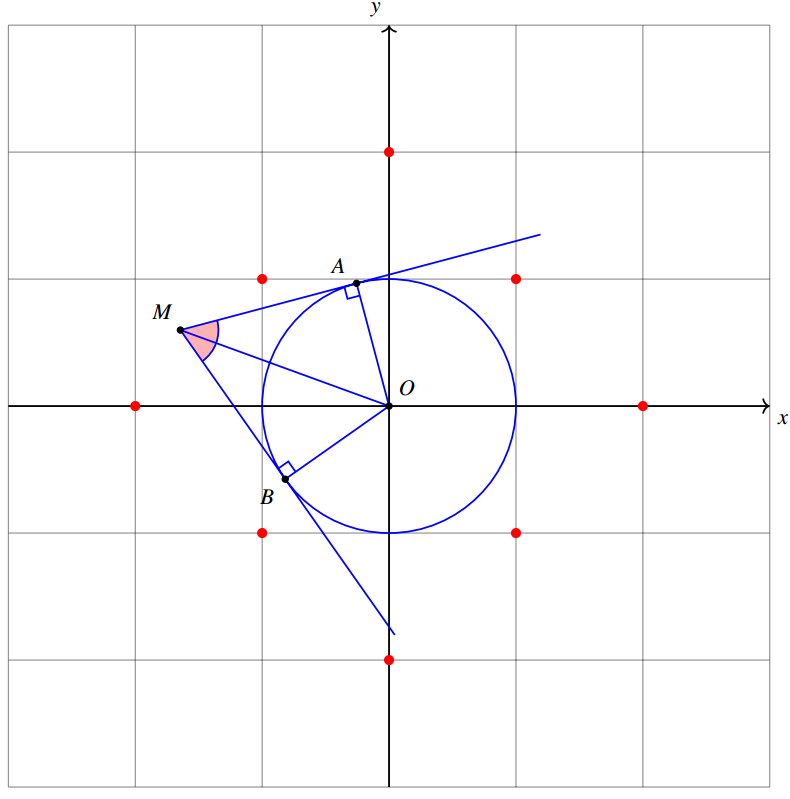
Để từ \(M\) kẻ được \(2\) tiếp tuyến \(MA\), \(MB\) đến \(\left( C \right)\), suy ra \(OM > 1\).
Dễ thấy \(\widehat {AMO} = \widehat {BMO} = \frac{{\widehat {AMB}}}{2} \Rightarrow \widehat {AMB} \ge 60^\circ \Leftrightarrow \widehat {AMO} \ge 30^\circ \).
Trong \(\Delta AMO\) vuông tại \(A\):
\(30^\circ \le \widehat {AMO} < 90^\circ \Rightarrow \sin 30^\circ \le \sin AMO < \sin 90^\circ \Leftrightarrow \frac{1}{2} \le \frac{{OA}}{{OM}} < 1 \Rightarrow 1 < OM \le 2\).
Do đó: \(1 < \sqrt {{x^2} + {y^2}} \le 2 \Rightarrow 1 < {x^2} + {y^2} \le 4\). Do \(x,y \in \mathbb{Z}\) nên có hai trường hợp:
· \({x^2} + {y^2} = 2\): Có \(4\) điểm \(\left( {x;y} \right) \in \left\{ {\left( {1;1} \right);\left( { - 1;1} \right);\left( {1; - 1} \right);\left( { - 1; - 1} \right)} \right\}\).
· \({x^2} + {y^2} = 4\): Có \(4\) điểm \(\left( {x;y} \right) \in \left\{ {\left( {2;0} \right);\left( { - 2;0} \right);\left( {0;2} \right);\left( {0; - 2} \right)} \right\}\).
Vậy có \(8\) điểm \(M\) thỏa mãn hay số phần tử của \(T\) là \(8\).
Số cách chọn ngẫu nhiên \(2\) điểm trong \(T\): \(C_8^2 = 28\).
Để đường thẳng đi qua \(2\) điểm được chọn song song với trục \(Ox\) có \(2\) trường hợp thỏa mãn: \(\left( {1;1} \right)\) và \(\left( { - 1;1} \right)\); \(\left( {1; - 1} \right)\) và \(\left( { - 1; - 1} \right)\).
Vậy xác suất cần tìm: \(P = \frac{2}{{28}} = \frac{1}{{14}} \Rightarrow \frac{1}{a} = \frac{1}{{14}} \Rightarrow a = 14 \Rightarrow {a^2} = 196\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) Sai.
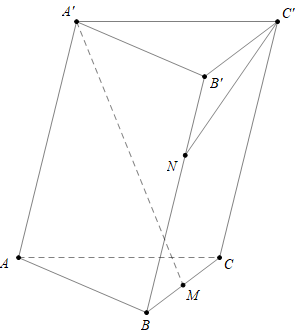
Ta có: \(\overrightarrow {A'M} = \frac{1}{2}\left( {\overrightarrow {A'B} + \overrightarrow {A'C} } \right)\)\( = \frac{1}{2}\left( {\overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'A} + \overrightarrow {A'C'} } \right) = \overrightarrow {A'A} + \frac{1}{2}\overrightarrow {A'B'} + \frac{1}{2}\overrightarrow {A'C'} \)\( = \frac{1}{2}.\overrightarrow {AB} + \frac{1}{2}.\overrightarrow {AC} - \overrightarrow {AA'} \). Suy ra \(x = y = \frac{1}{2};z = - 1 \Rightarrow x + y = - z\).
b) Đúng.
Ta có: \(\overrightarrow {BN} = \frac{2}{3}\overrightarrow {BB'} \Leftrightarrow \overrightarrow {BN} = \frac{2}{3}\left( {\overrightarrow {BN} + \overrightarrow {NB'} } \right) \Leftrightarrow \overrightarrow {BN} = 2\overrightarrow {NB'} \Leftrightarrow \overrightarrow {NB} = - 2\overrightarrow {NB'} \).
c) Đúng.
Ta có: \(\overrightarrow {AB} + \overrightarrow {CC'} = \overrightarrow {AB} + \overrightarrow {BB'} = \overrightarrow {AB'} \).
d) Đúng.
Ta có:\(\overrightarrow {C'N} = \overrightarrow {C'B'} + \overrightarrow {B'N} = \overrightarrow {A'B'} - \overrightarrow {A'C'} + \frac{1}{3}\overrightarrow {B'B} = \overrightarrow {AB} - \overrightarrow {AC} - \frac{1}{3}\overrightarrow {AA'} \)\( \Rightarrow \overrightarrow {A'M} .\overrightarrow {C'N} = \left( {\frac{1}{2}.\overrightarrow {AB} + \frac{1}{2}.\overrightarrow {AC} - \overrightarrow {AA'} } \right).\left( {\overrightarrow {AB} - \overrightarrow {AC} - \frac{1}{3}\overrightarrow {AA'} } \right)\)\( = \frac{1}{2}A{B^2} - \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AC} - \frac{1}{6}\overrightarrow {AB} .\overrightarrow {AA'} + \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AB} - \frac{1}{2}A{C^2} - \frac{1}{6}\overrightarrow {AC} .\overrightarrow {AA'} - \overrightarrow {AA'} .\overrightarrow {AB} + \overrightarrow {AA'} .\overrightarrow {AC} + \frac{1}{3}A{A'^2}\)
\( = \frac{1}{2}A{B^2} - \frac{1}{2}A{C^2} + \frac{1}{3}A{A'^2} - \frac{7}{6}\overrightarrow {AB} .\overrightarrow {AA'} + \frac{5}{6}\overrightarrow {AC} .\overrightarrow {AA'} \)
\( = = \frac{1}{2}{a^2} - \frac{1}{2}{a^2} + \frac{1}{3}{a^2} - \frac{7}{6}\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AA'} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AA'} } \right) + \frac{5}{6}\left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AA'} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {AA'} } \right)\)
\( = \frac{1}{3}{a^2} - \frac{7}{6}{a^2}.\cos \widehat {A'AB} + \frac{5}{6}{a^2}.\cos \widehat {A'AC} = \frac{1}{3}{a^2} - \frac{7}{6}{a^2}.\cos 120^\circ + \frac{5}{6}{a^2}.\cos 60^\circ \)
\( = \frac{4}{3}{a^2}\).
Lời giải
Đáp án: 1,65.
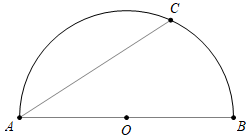
Đặt \(\widehat {CAB} = \varphi \left( {rad} \right)\), \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
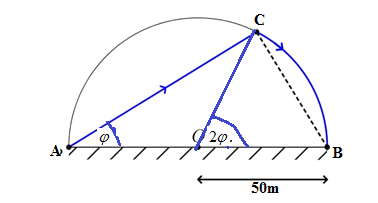
Ta có \(\Delta ABC\) vuông tại \(C\) \( \Rightarrow AC = AB.\cos \varphi = 0,1\cos \varphi \).
Mà \(\widehat {COR} = 2\widehat {CAB} = 2\varphi \).
Độ dài cung tròn .
Tổng thời gian người này di chuyển từ \(A\) đến \(C\) và đến B là: với \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
\( \Rightarrow t'\left( \varphi \right) = - \frac{1}{{50}}\sin \varphi + \frac{1}{{60}} = 0 \Leftrightarrow \sin \varphi = \frac{5}{6} \Rightarrow \varphi \approx 0,985\) rad.
Bảng biến thiên
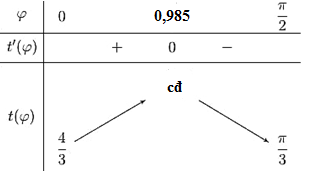
Vậy thời gian tối đa để di chuyển từ \(A\) đến \(C\)và đến B là \(t\left( {0,985} \right) = 0,027\)(giờ)\( \simeq 1,65\)phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.