Một cái lều có dạng hình chóp tứ giác đều, cạnh đáy bằng \(8{\rm{ m}}\) và chiều cao là \(3{\rm{ m}}{\rm{.}}\) Cửa vào lều là hình thang \(EFGH\) trong đó \(AE = FB\) và \(EF = 4{\rm{ m}}{\rm{.}}\) Gọi \(G,H\) lần lượt là trung điểm của \(SE\) và \(SF.\) Một nguồn sáng đặt cách đỉnh \(S\) một mét ở phía dưới. Ánh sáng chiếu ra ngoài qua cửa tạo thành một vùng được chiếu sáng \(EFG'H'.\) Diện tích vùng được chiếu sáng là bao nhiêu \({{\rm{m}}^2}\) (Làm tròn kết quả đến hàng đơn vị)?
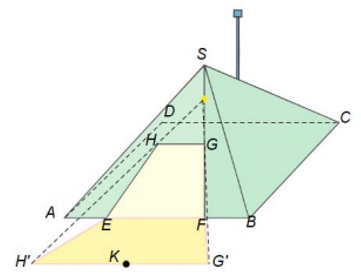
Một cái lều có dạng hình chóp tứ giác đều, cạnh đáy bằng \(8{\rm{ m}}\) và chiều cao là \(3{\rm{ m}}{\rm{.}}\) Cửa vào lều là hình thang \(EFGH\) trong đó \(AE = FB\) và \(EF = 4{\rm{ m}}{\rm{.}}\) Gọi \(G,H\) lần lượt là trung điểm của \(SE\) và \(SF.\) Một nguồn sáng đặt cách đỉnh \(S\) một mét ở phía dưới. Ánh sáng chiếu ra ngoài qua cửa tạo thành một vùng được chiếu sáng \(EFG'H'.\) Diện tích vùng được chiếu sáng là bao nhiêu \({{\rm{m}}^2}\) (Làm tròn kết quả đến hàng đơn vị)?

Quảng cáo
Trả lời:
Đáp án:
Gọi \(I\) là điểm phát sáng; \(M\) là trung điểm của \(EF;N = SM \cap GH;K = OM \cap G'H'.\)
Ta có \(GH\) là đường trung bình của tam giác \(SEF\) nên
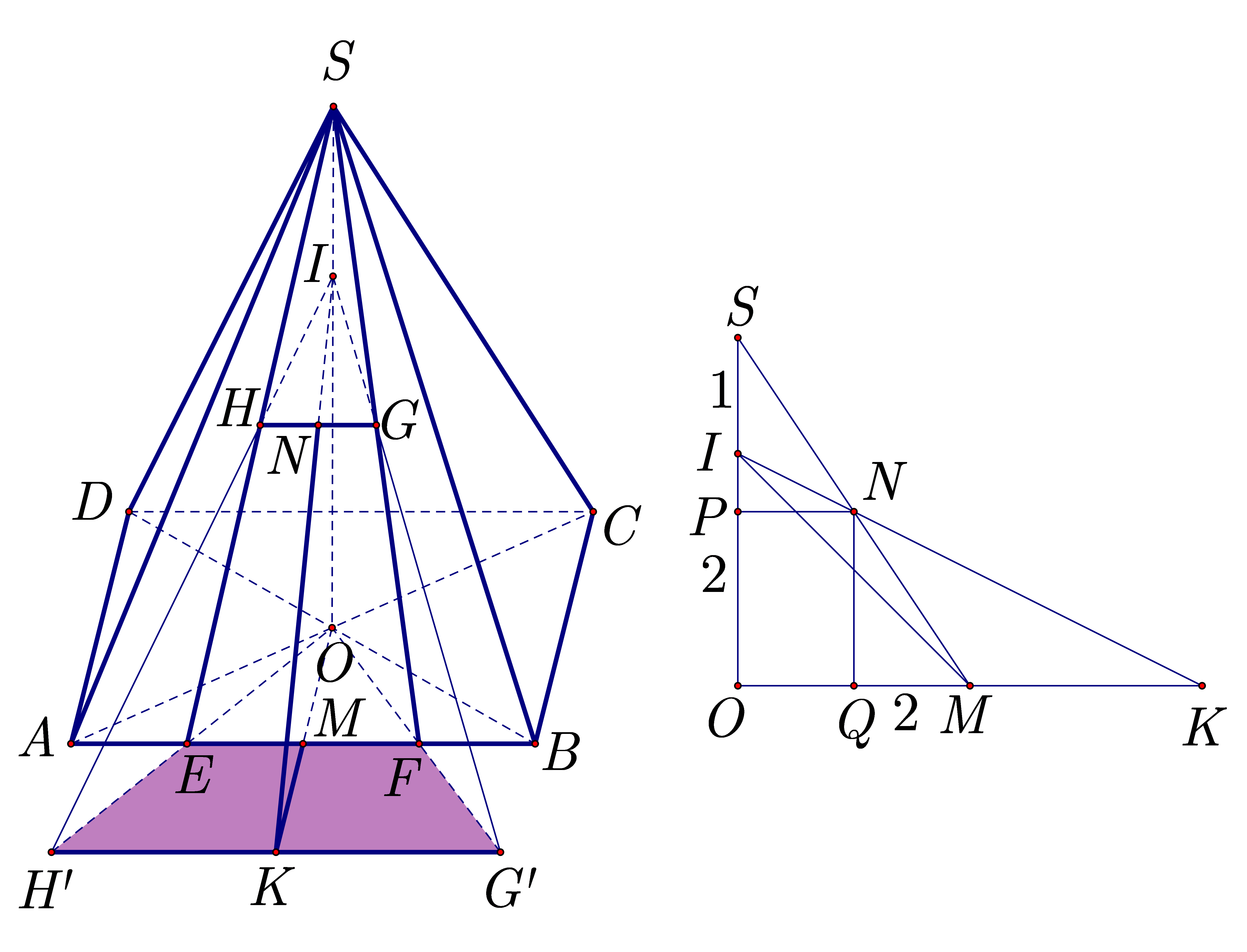
Gọi \(P,Q\) lần lượt là trung điểm của \(SO,OM.\) Theo đề bài ta có
\(SI = 1{\rm{m,}}IO = 2{\rm{m,}}SP = \frac{1}{2}SO = \frac{3}{2}{\rm{m}} \Rightarrow IP = \frac{1}{2};NP = OQ = 2{\rm{m}}\) (vì \(M\) là trung điểm của \(EF\) nên \(N\) là trung điểm của \(GH,SM)\)
Xét tam giác \(IOK\) có
Mà \(OM = 4\) nên \(M\) là trung điểm của \(OK\) và nên \(EF\) là đường trung bình của tam giác \(OG'H' \Rightarrow G'H' = 2EF = 2(AB - AE - FB) = 8{\rm{ m}}{\rm{.}}\)
Do \(M\) là trung điểm của \(EF\), cũng là trung điểm của \(AB\) nên \(OM \bot EF.\) Suy ra \(MK\) là đường cao của hình thang \(EFG'H'\) và \(MK = OM = 4{\rm{ m}}{\rm{.}}\)
Vậy \({S_{EFG'H'}} = \frac{{EF + G'H'}}{2}.MK = \frac{{4 + 8}}{2}.4 = 24{\rm{ }}{{\rm{m}}^2}.\)
Cách khác
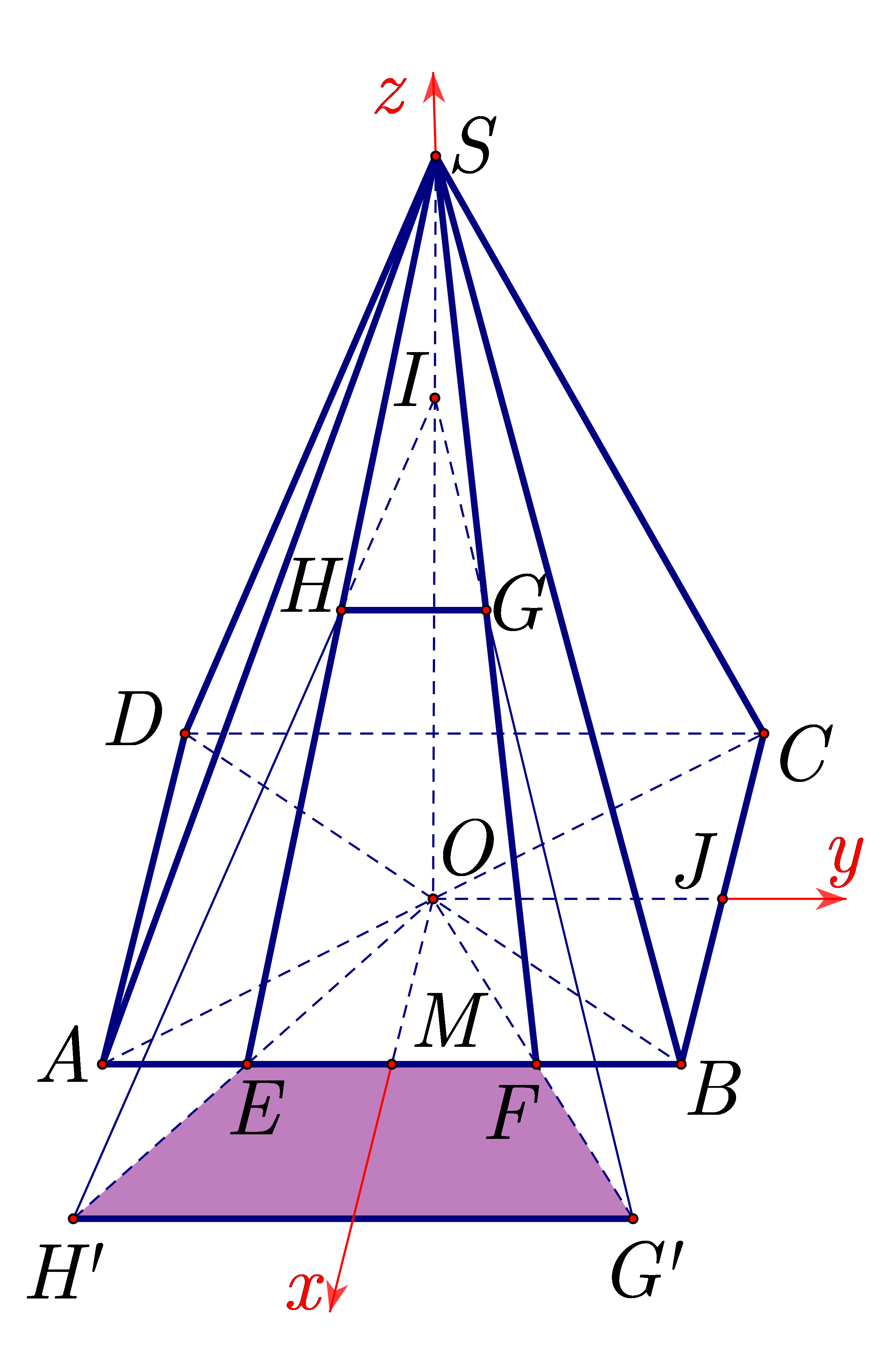
Gọi \(I\) là điểm phát sáng; \(M\) là trung điểm của \(EF\) cũng là trung điểm của \(AB({\rm{v\`i }}AE = FB);J\) là trung điểm của \(BC\) (hình vẽ).
Chọn hệ trục tọa độ \(Oxyz\) sao cho tia \(OM \equiv Ox,ON \equiv Oy,OS \equiv Oz.\) Khi đó
\(O(0;0;0),M(4;0;0),J(0;4;0),S(0;0;3);A(4; - 4;0);B(4;4;0);E(4; - 2;0),F(4;2;0),I(0;0;2).\)
\(H\) là trung điểm \(SE \Rightarrow H\left( {2; - 1;\frac{3}{2}} \right)\); \(G\)là trung điểm của \(SF \Rightarrow G\left( {2;1;\frac{3}{2}} \right).\)
\({\rm{Mp}}(ABCD) \equiv Oxy:z = 0.\)
\(\overrightarrow {IH} = \left( {2; - 1; - \frac{1}{2}} \right) = \frac{1}{2}(4; - 2; - 1) \Rightarrow IH:\left\{ \begin{array}{l}x = 4t\\y = - 2t\\z = 2 - t\end{array} \right. \Rightarrow H' = IH \cap Oxy \Rightarrow H'(8; - 4;0)\)
\(\overrightarrow {IG} = \left( {2;1; - \frac{1}{2}} \right) = \frac{1}{2}(4;2; - 1) \Rightarrow IG:\left\{ \begin{array}{l}x = 4t'\\y = 2t'\\z = 2 - t'\end{array} \right. \Rightarrow G = IG \cap Oxy \Rightarrow G(8;4;0)\)
\(\overrightarrow {EH'} = (4; - 2;0),\overrightarrow {EG'} = (4;6;0),\overrightarrow {EF} = (0;4;0)\)
Vậy
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) Sai.
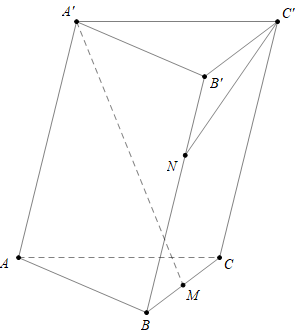
Ta có: \(\overrightarrow {A'M} = \frac{1}{2}\left( {\overrightarrow {A'B} + \overrightarrow {A'C} } \right)\)\( = \frac{1}{2}\left( {\overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'A} + \overrightarrow {A'C'} } \right) = \overrightarrow {A'A} + \frac{1}{2}\overrightarrow {A'B'} + \frac{1}{2}\overrightarrow {A'C'} \)\( = \frac{1}{2}.\overrightarrow {AB} + \frac{1}{2}.\overrightarrow {AC} - \overrightarrow {AA'} \). Suy ra \(x = y = \frac{1}{2};z = - 1 \Rightarrow x + y = - z\).
b) Đúng.
Ta có: \(\overrightarrow {BN} = \frac{2}{3}\overrightarrow {BB'} \Leftrightarrow \overrightarrow {BN} = \frac{2}{3}\left( {\overrightarrow {BN} + \overrightarrow {NB'} } \right) \Leftrightarrow \overrightarrow {BN} = 2\overrightarrow {NB'} \Leftrightarrow \overrightarrow {NB} = - 2\overrightarrow {NB'} \).
c) Đúng.
Ta có: \(\overrightarrow {AB} + \overrightarrow {CC'} = \overrightarrow {AB} + \overrightarrow {BB'} = \overrightarrow {AB'} \).
d) Đúng.
Ta có:\(\overrightarrow {C'N} = \overrightarrow {C'B'} + \overrightarrow {B'N} = \overrightarrow {A'B'} - \overrightarrow {A'C'} + \frac{1}{3}\overrightarrow {B'B} = \overrightarrow {AB} - \overrightarrow {AC} - \frac{1}{3}\overrightarrow {AA'} \)\( \Rightarrow \overrightarrow {A'M} .\overrightarrow {C'N} = \left( {\frac{1}{2}.\overrightarrow {AB} + \frac{1}{2}.\overrightarrow {AC} - \overrightarrow {AA'} } \right).\left( {\overrightarrow {AB} - \overrightarrow {AC} - \frac{1}{3}\overrightarrow {AA'} } \right)\)\( = \frac{1}{2}A{B^2} - \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AC} - \frac{1}{6}\overrightarrow {AB} .\overrightarrow {AA'} + \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AB} - \frac{1}{2}A{C^2} - \frac{1}{6}\overrightarrow {AC} .\overrightarrow {AA'} - \overrightarrow {AA'} .\overrightarrow {AB} + \overrightarrow {AA'} .\overrightarrow {AC} + \frac{1}{3}A{A'^2}\)
\( = \frac{1}{2}A{B^2} - \frac{1}{2}A{C^2} + \frac{1}{3}A{A'^2} - \frac{7}{6}\overrightarrow {AB} .\overrightarrow {AA'} + \frac{5}{6}\overrightarrow {AC} .\overrightarrow {AA'} \)
\( = = \frac{1}{2}{a^2} - \frac{1}{2}{a^2} + \frac{1}{3}{a^2} - \frac{7}{6}\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AA'} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AA'} } \right) + \frac{5}{6}\left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AA'} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {AA'} } \right)\)
\( = \frac{1}{3}{a^2} - \frac{7}{6}{a^2}.\cos \widehat {A'AB} + \frac{5}{6}{a^2}.\cos \widehat {A'AC} = \frac{1}{3}{a^2} - \frac{7}{6}{a^2}.\cos 120^\circ + \frac{5}{6}{a^2}.\cos 60^\circ \)
\( = \frac{4}{3}{a^2}\).
Lời giải
Đáp án: 1,65.
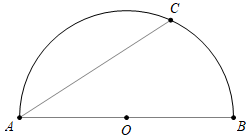
Đặt \(\widehat {CAB} = \varphi \left( {rad} \right)\), \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
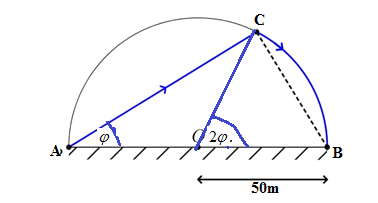
Ta có \(\Delta ABC\) vuông tại \(C\) \( \Rightarrow AC = AB.\cos \varphi = 0,1\cos \varphi \).
Mà \(\widehat {COR} = 2\widehat {CAB} = 2\varphi \).
Độ dài cung tròn .
Tổng thời gian người này di chuyển từ \(A\) đến \(C\) và đến B là: với \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
\( \Rightarrow t'\left( \varphi \right) = - \frac{1}{{50}}\sin \varphi + \frac{1}{{60}} = 0 \Leftrightarrow \sin \varphi = \frac{5}{6} \Rightarrow \varphi \approx 0,985\) rad.
Bảng biến thiên
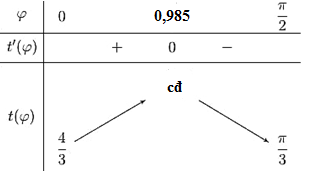
Vậy thời gian tối đa để di chuyển từ \(A\) đến \(C\)và đến B là \(t\left( {0,985} \right) = 0,027\)(giờ)\( \simeq 1,65\)phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.