Trong đề kiểm tra 15 phút môn Toán của lớp 11A có 20 câu trắc nghiệm. Mỗi câu trắc nghiệm có 4 phương án trả lời, trong đó chỉ có một phương án trả lời đúng. Biết rằng mỗi câu trả lời đúng được 0,5 điểm. Nam giải chắc chắn đúng 10 câu, 10 câu còn lại lựa chọn ngẫu nhiên đáp án. Biết rằng mỗi câu trả lời đúng được 0,5 điểm, trả lời sai không bị trừ điểm

Đáp số: 9.

Gọi \(x,y\)lần lượt là số xe loại A và B mà đại lý cần thuê. ĐK \(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\end{array} \right.\)

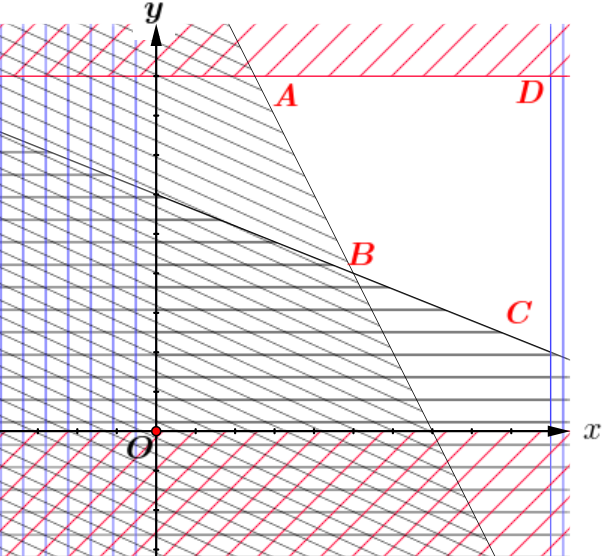
Từ đề bài ta có: \(\left\{ \begin{array}{l}20{\rm{x}} + 10y \ge 140\\0,6{\rm{x}} + 1,5y \ge 9\end{array} \right.\).

Khi đó, số tiền thuê xe là: \(T = 5x + 4,5y\).

Miền nghiệm \(\left( {x,y} \right)\)là tứ giác \(ABC{\rm{D}}\) với \(A(\frac{5}{2};9),\,\,\,B(5;4),\,\,C(10;2),\,\,D(10;9).\)

Tại đỉnh \(B\)thì \(T = 43\) đạt giá trị nhỏ nhất nên \(x = 5,y = 4 \Rightarrow 2x + y = 14.\)

Đáp án: 1

Tọa độ hai điểm cực trị của đồ thị hàm số \(y = {x^3} - 3x\) là \(\left( { - 1;2} \right);\left( {1; - 2} \right)\)

Phương trình đường thẳng đi qua 2 điểm cực trị \(2x + y = 0\)(d)

Hai điểm A, B nằm cùng phía đối với d . Gọi \(A'\) là điểm đối xứng với A qua d.

Khi đó \[MA{\rm{ }} + {\rm{ }}MB = MA'{\rm{ }} + {\rm{ }}MB \ge A'B\].

Do đó \[MA{\rm{ }} + {\rm{ }}MB\] ngắn nhất thì \(M,A',B\)thẳng hàng hay \(M = A'B \cap d\).

\(\Delta \) là đường thẳng đi qua A và vuông góc d

PT \(\Delta \) \(\left( {x - 1} \right) - 2\left( {y - 2} \right) = 0\)\( \Leftrightarrow x - 2y + 3 = 0\)

Gọi I là giao điểm của d và \(\Delta \)\( \Rightarrow I\left( { - \frac{3}{5};\frac{6}{5}} \right)\)\( \Rightarrow A'\left( { - \frac{{11}}{5};\frac{2}{5}} \right)\).

\(\overrightarrow {A'B}  = \left( {\frac{{21}}{5};\frac{3}{5}} \right) \Rightarrow \)VTPT của \(A'B\)là \(\overrightarrow n \left( {3; - 21} \right)\)

PT \(A'B\):\(3\left( {x - 2} \right) - 21\left( {y - 1} \right) = 0\)  \( \Leftrightarrow 3x - 21y + 15 = 0\)

\(M = A'B \cap d \Rightarrow M\left( { - \frac{1}{3};\frac{2}{3}} \right)\)nên \(a =  - \frac{1}{3};b = \frac{2}{3}\)

Khi đó \(b - a = \frac{2}{3} - \left( { - \frac{1}{3}} \right) = 1\).