Cho hai biểu thức \(P = \left( {\frac{{x - 6\sqrt x  + 1}}{{x - 1}} - \frac{{\sqrt x  - 1}}{{\sqrt x  + 1}}} \right):\frac{{x + 4}}{{1 - x}}\) và \(Q = \frac{{\sqrt x }}{{x + 4}}\) (với \(x \ge 0;x \ne 1\)).

a)  Tính giá trị biểu thức \(Q\)  với \(x = 4\)          .

b) Chứng minh rằng \(P = 4Q\).

c) Tìm tất cả các giá trị của \(x\) để \(P\) nhận giá trị là số nguyên.

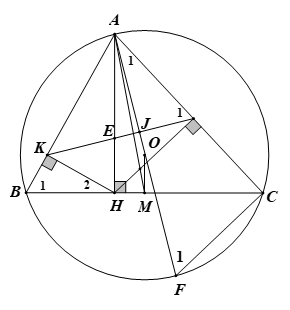
1.a)  Chứng minh tứ giác \(AKHI\)nội tiếp đường tròn.

Ta có:

\(\widehat {AKH} = 90^\circ \)(vì \(HK\) vuông góc với \(AB\) tại \(K\))

\(\widehat {AIH} = 90^\circ \)(vì\(HI\) vuông góc với \(AC\) tại \(I\)).

 Xét tứ giác\(AKHI\)có: \(\widehat {AKH}\,\, + \,\widehat {AIH} = 90^\circ  + 90^\circ  = 180^\circ \), mà hai góc này ở vị trí đối nhau.

Vậy tứ giác \(AKHI\)nội tiếp đường tròn.

b) Gọi \(E\) là giao điểm của\(AH\)với \(KI\). Chứng minh rằng \(EA.EH = EK.EI\).

Vì tứ giác \(AKHI\)nội tiếp đường tròn (cmt) nên \(\widehat {HKI} = \widehat {HAI}\)(hai góc nội tiếp cùng chắn )

Hay \(\widehat {HKE} = \widehat {IAE}\).

Xét \(\Delta EKH\) và \(\Delta EAI\)có:

\(\widehat {KEH} = \widehat {AEI}\)(hai góc đối đỉnh);

\(\widehat {HKE} = \widehat {IAE}\)(cmt)

Do đó: (g.g)

\( \Rightarrow \frac{{EK}}{{EA}} = \frac{{EH}}{{EI}} \Rightarrow EA.EH = EK.EI\)

Vậy ta có điều phải chứng minh.

c) Chứng minh \(KI\)vuông góc với \(AO\).

Kẻ đường kính \[AF\] của đường tròn \(\left( {O;R} \right)\); Gọi J là giao điểm của \(KI\) và \(AO\)

Xét đường tròn \(\left( {O;R} \right)\)có \({\widehat F_1} = {\widehat B_1}\)(hai góc nội tiếp cùng chắn cung \(AC\)). (1)

Lại có \({\widehat B_1} = {\widehat H_1}\) (vì cùng phụ với \({\widehat H_2}\)). (2)

Vì tứ giác \(AKHI\)nội tiếp đường tròn (cmt)

nên \({\widehat H_1} = {\widehat I_1}\) (hai góc nội tiếp cùng chắn cung\(AK\))  (3).

Từ (1); (2) và (3) suy ra: \(\widehat {{F_1}} = {\widehat I_1}\).

Mà trong đường tròn \(\left( {O;R} \right)\)có:\(\widehat {ACF} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn).

Hay\({\widehat A_1} + {\widehat F_1} = 90^\circ \) (4).

Từ (3) và (4) suy ra \({\widehat A_1} + {\widehat I_1} = 90^\circ \)\( \Rightarrow \widehat {AJI} = 90^\circ \).

Vậy \(KI\)vuông góc với \(AO\).

d)  Giả sử điểm \(A\) và  đường tròn \(\left( {O;R} \right)\) cố định, còn dây \(BC\) thay đổi sao cho \(AB.AC = 3{R^2}\).

Xác định vị trí của dây cung \(BC\) sao cho tam giác \(ABC\) có diện tích lớn nhất.

Có \(\widehat {ACF} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

 \(\widehat {ABH} = \widehat {AFC}\)(hai góc nội tiếp cùng chắn cung  của đường tròn \(\left( {O;R} \right)\)

Xét \(\Delta AHB\) và \(\Delta ACF\)có:

\(\widehat {AHB} = \widehat {ACF}\left( {{{90}^0}} \right)\);

\(\widehat {ABH} = \widehat {AFC}\)(cmt)

Do đó: (g.g) \( \Rightarrow \frac{{AH}}{{AC}} = \frac{{AB}}{{AF}} \Rightarrow AH = \frac{{AB.AC}}{{AF}} = \frac{{3{R^2}}}{{2R}} = \frac{{3R}}{2}\)

 Ta có: \({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}.\frac{{3R}}{2}.BC = \frac{{3R}}{4}.BC\).

Do \(R\) không đổi nên \({S_{ABC}}\)lớn nhất \( \Leftrightarrow BC\) lớn nhất.

Gọi \(M\) là trung điểm của \(BC\) thì .

\(BC\) lớn nhất \( \Leftrightarrow OM\) bé nhất.

Ta có \(OM \ge AM - AO \ge AH - AO = \frac{{3R}}{2} - R = \frac{R}{2}\).

\(OM\) bé nhất bằng \(\frac{R}{2}\)\( \Leftrightarrow A,O,M\)thẳng hàng và \(H \equiv M\).

Khi đó \(AH = AM = AO + OM = R + \frac{R}{2} = \frac{{3R}}{2}\)

Vậy diện tích \(\Delta ABC\) lớn nhất khi \(BC\)cách \(A\) một khoảng bằng \(\frac{{3R}}{2}\) (\(\Delta ABC\) đều)

2) Gọi bán kính đáy của hình nón là \(R\).

Do diện tích của đáy hình nón là \(S = 16\pi  \Rightarrow \pi {R^2} = 16\pi  \Rightarrow R = 4{\rm{ }}\left( {cm} \right)\)

Theo giả thiết chiều cao của hình nón gấp 3 lần bán kính đáy nên chiều cao của hình nón là: \(h = 3R = 3.4 = 12{\rm{ }}\left( {cm} \right)\)

Thể tích hình nón là: \(V = \frac{1}{3}S.h = \frac{1}{3}.16\pi .12{\rm{  = 64}}\pi \left( {c{m^3}} \right)\)

Vậy thể tích hình nón là \({\rm{64}}\pi c{m^3}\)