1) Cho tam giác \(ABC\) nhọn, nội tiếp đường tròn \(\left( {O;R} \right)\). Kẻ \(AH\) vuông góc với \(BC\) tại \(H\),   \(HK\) vuông góc với \(AB\) tại \(K\) và \(HI\) vuông góc với \(AC\) tại \(I\),.

a)  Chứng minh tứ giác \(AKHI\)nội tiếp đường tròn.

b) Gọi \(E\) là giao điểm của\(AH\)với \(KI\). Chứng minh rằng \(EA.EH = EK.EI\).

c) Chứng minh \(KI\)vuông góc với \(AO\).

d)  Giả sử điểm \(A\) và  đường tròn \(\left( {O;R} \right)\) cố định, còn dây \(BC\) thay đổi sao cho \(AB.AC = 3{R^2}\). Xác định vị trí của dây cung \(BC\) sao cho tam giác \(ABC\) có diện tích lớn nhất.

2) Một hình nón có diện tích đáy bằng \(16\pi \left( {c{m^2}} \right)\) và có chiều cao gấp ba lần bán kính đáy. Tính thể tích của hình nón đó.

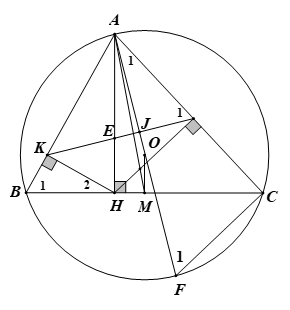
1.a)  Chứng minh tứ giác \(AKHI\)nội tiếp đường tròn.

Ta có:

\(\widehat {AKH} = 90^\circ \)(vì \(HK\) vuông góc với \(AB\) tại \(K\))

\(\widehat {AIH} = 90^\circ \)(vì\(HI\) vuông góc với \(AC\) tại \(I\)).

 Xét tứ giác\(AKHI\)có: \(\widehat {AKH}\,\, + \,\widehat {AIH} = 90^\circ  + 90^\circ  = 180^\circ \), mà hai góc này ở vị trí đối nhau.

Vậy tứ giác \(AKHI\)nội tiếp đường tròn.

b) Gọi \(E\) là giao điểm của\(AH\)với \(KI\). Chứng minh rằng \(EA.EH = EK.EI\).

Vì tứ giác \(AKHI\)nội tiếp đường tròn (cmt) nên \(\widehat {HKI} = \widehat {HAI}\)(hai góc nội tiếp cùng chắn )

Hay \(\widehat {HKE} = \widehat {IAE}\).

Xét \(\Delta EKH\) và \(\Delta EAI\)có:

\(\widehat {KEH} = \widehat {AEI}\)(hai góc đối đỉnh);

\(\widehat {HKE} = \widehat {IAE}\)(cmt)

Do đó: (g.g)

\( \Rightarrow \frac{{EK}}{{EA}} = \frac{{EH}}{{EI}} \Rightarrow EA.EH = EK.EI\)

Vậy ta có điều phải chứng minh.

c) Chứng minh \(KI\)vuông góc với \(AO\).

Kẻ đường kính \[AF\] của đường tròn \(\left( {O;R} \right)\); Gọi J là giao điểm của \(KI\) và \(AO\)

Xét đường tròn \(\left( {O;R} \right)\)có \({\widehat F_1} = {\widehat B_1}\)(hai góc nội tiếp cùng chắn cung \(AC\)). (1)

Lại có \({\widehat B_1} = {\widehat H_1}\) (vì cùng phụ với \({\widehat H_2}\)). (2)

Vì tứ giác \(AKHI\)nội tiếp đường tròn (cmt)

nên \({\widehat H_1} = {\widehat I_1}\) (hai góc nội tiếp cùng chắn cung\(AK\))  (3).

Từ (1); (2) và (3) suy ra: \(\widehat {{F_1}} = {\widehat I_1}\).

Mà trong đường tròn \(\left( {O;R} \right)\)có:\(\widehat {ACF} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn).

Hay\({\widehat A_1} + {\widehat F_1} = 90^\circ \) (4).

Từ (3) và (4) suy ra \({\widehat A_1} + {\widehat I_1} = 90^\circ \)\( \Rightarrow \widehat {AJI} = 90^\circ \).

Vậy \(KI\)vuông góc với \(AO\).

d)  Giả sử điểm \(A\) và  đường tròn \(\left( {O;R} \right)\) cố định, còn dây \(BC\) thay đổi sao cho \(AB.AC = 3{R^2}\).

Xác định vị trí của dây cung \(BC\) sao cho tam giác \(ABC\) có diện tích lớn nhất.

Có \(\widehat {ACF} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

 \(\widehat {ABH} = \widehat {AFC}\)(hai góc nội tiếp cùng chắn cung  của đường tròn \(\left( {O;R} \right)\)

Xét \(\Delta AHB\) và \(\Delta ACF\)có:

\(\widehat {AHB} = \widehat {ACF}\left( {{{90}^0}} \right)\);

\(\widehat {ABH} = \widehat {AFC}\)(cmt)

Do đó: (g.g) \( \Rightarrow \frac{{AH}}{{AC}} = \frac{{AB}}{{AF}} \Rightarrow AH = \frac{{AB.AC}}{{AF}} = \frac{{3{R^2}}}{{2R}} = \frac{{3R}}{2}\)

 Ta có: \({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}.\frac{{3R}}{2}.BC = \frac{{3R}}{4}.BC\).

Do \(R\) không đổi nên \({S_{ABC}}\)lớn nhất \( \Leftrightarrow BC\) lớn nhất.

Gọi \(M\) là trung điểm của \(BC\) thì .

\(BC\) lớn nhất \( \Leftrightarrow OM\) bé nhất.

Ta có \(OM \ge AM - AO \ge AH - AO = \frac{{3R}}{2} - R = \frac{R}{2}\).

\(OM\) bé nhất bằng \(\frac{R}{2}\)\( \Leftrightarrow A,O,M\)thẳng hàng và \(H \equiv M\).

Khi đó \(AH = AM = AO + OM = R + \frac{R}{2} = \frac{{3R}}{2}\)

Vậy diện tích \(\Delta ABC\) lớn nhất khi \(BC\)cách \(A\) một khoảng bằng \(\frac{{3R}}{2}\) (\(\Delta ABC\) đều)

2) Gọi bán kính đáy của hình nón là \(R\).

Do diện tích của đáy hình nón là \(S = 16\pi  \Rightarrow \pi {R^2} = 16\pi  \Rightarrow R = 4{\rm{ }}\left( {cm} \right)\)

Theo giả thiết chiều cao của hình nón gấp 3 lần bán kính đáy nên chiều cao của hình nón là: \(h = 3R = 3.4 = 12{\rm{ }}\left( {cm} \right)\)

Thể tích hình nón là: \(V = \frac{1}{3}S.h = \frac{1}{3}.16\pi .12{\rm{  = 64}}\pi \left( {c{m^3}} \right)\)

Vậy thể tích hình nón là \({\rm{64}}\pi c{m^3}\)