Cho tứ diện đều \(ABCD\) có cạnh bằng 1. Gọi \(M,N\) là hai điểm thay đổi lần lượt thuộc các cạnh \(AB;AC\) sao cho mặt phẳng \(\left( {DMN} \right)\) luôn vuông góc với mặt phẳng \(\left( {ABC} \right)\). Đặt \(AM = x;AN = y\). Tìm cặp số \(\left( {x;y} \right)\) để tam giác \(DMN\) có diện tích nhỏ nhất.
Quảng cáo
Trả lời:
Đáp án đúng là A
Phương pháp giải
Sử dụng bất đẳng thức
Lời giải
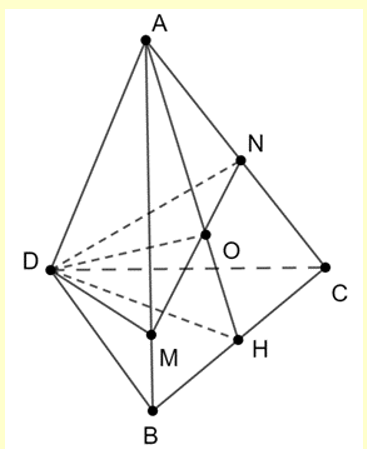
Gọi \(O\) là tâm đường tròn ngoại tiếp của tam giác đều \(ABC\). Do \(ABCD\) là tứ diện đều nên \(DO \bot \left( {ABC} \right)\). Theo đề bài, mặt phẳng \(\left( {DMN} \right) \bot \left( {ABC} \right)\) nên suy ra \(O \in MN\).
Tam giác \(DMN\) có \(DO \bot MN\) nên \({S_{\Delta DMN}} = \frac{1}{2}DO.MN\). Mà \(DO\) là hằng số nên \({S_{\Delta DMN}}\) lớn nhất khi \(MN\) lớn nhất, nhỏ nhất khi \(MN\) nhỏ nhất.
Áp dụng định lí cosin trong tam giác \(AMN\) ta có \(M{N^2} = {x^2} + {y^2} - xy = {(x + y)^2} - 3xy\).
Như vậy \(M,N\) thay đổi sao cho đoạn thẳng \(MN\) luôn đi qua \(O\). Ta có \(0 < x,y \le 1\).
Ta có \(\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = y\overrightarrow {AC} - x\overrightarrow {AB} \), \(\overrightarrow {MO} = \overrightarrow {AO} - \overrightarrow {AM} = \frac{2}{3}\overrightarrow {AH} - x\overrightarrow {AB} = \left( {\frac{1}{3} - x} \right)\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
Vì \(\overrightarrow {MN} \) và \(\overrightarrow {MO} \) cùng hướng nên \(\frac{{\frac{1}{3}}}{y} = \frac{{\frac{1}{3} - x}}{{ - x}} > 0 \Leftrightarrow y\left( {\frac{1}{3} - x} \right) = - \frac{1}{3}x \Leftrightarrow 3xy = x + y\) .
Từ \(0 < x,y \le 1\), ta có \(x + y = 3xy \Leftrightarrow \frac{1}{x} + \frac{1}{y} = 3 \Leftrightarrow \frac{1}{x} = 3 - \frac{1}{y} \Rightarrow \frac{1}{x} \le 2 \Leftrightarrow x \ge \frac{1}{2}\)
Ta có \(M{N^2} = {(x + y)^2} - \left( {x + y} \right)\).
Đặt \(t = x + y\). Ta có \(t = x + \frac{x}{{3x - 1}}\) với \(x \in \left[ {\frac{1}{2};1} \right],t'\left( x \right) = \frac{{3x\left( {3x - 2} \right)}}{{{{(3x - 1)}^2}}}\).
Vẽ bảng biến thiên và từ bảng biến thiên, ta có \(\frac{4}{3} \le t \le \frac{3}{2}\).
Ta có \(M{N^2} = f\left( t \right) = {t^2} - t\). Khảo sát sự biến thiên của hàm \(f\left( t \right)\) trên đoạn \(\left[ {\frac{4}{3};\frac{3}{2}} \right]\) ta được\(MN{\rm{min}} \Leftrightarrow t = \frac{4}{3} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{2}{3}}\\{y = \frac{2}{3}}\end{array}} \right.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
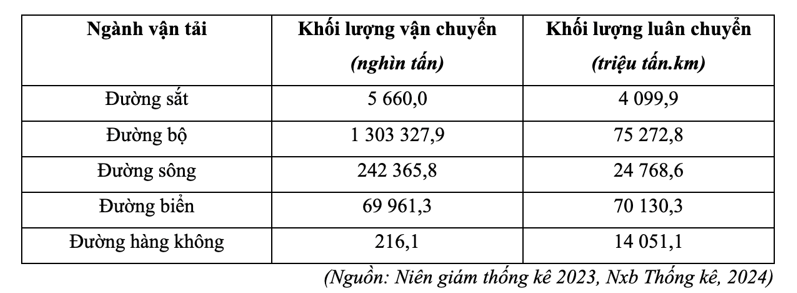
C. Đường sắt có cự li vận chuyển trung bình nhỏ hơn đường bộ.
Lời giải
Đáp án đúng là A
Phương pháp giải
Nhận xét bảng số liệu.
Lời giải
- Công thức:
Cự li vận chuyển trung bình = Khối lượng luân chuyển/Khối lượng vận chuyển.
- Dựa vào công thức tính trên, ta có bảng số liệu sau:
Cự li vận chuyển hàng hóa trung bình phân theo ngành vận tải của nước ta năm 2021
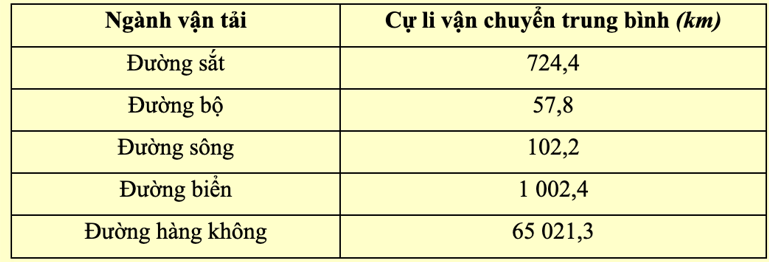
=> Đường hàng không có cự li vận chuyển trung bình dài nhất là nhận xét đúng.
Lời giải
Đáp án đúng là "2640"
Phương pháp giải
Tính giá trị nhỏ nhất
Lời giải
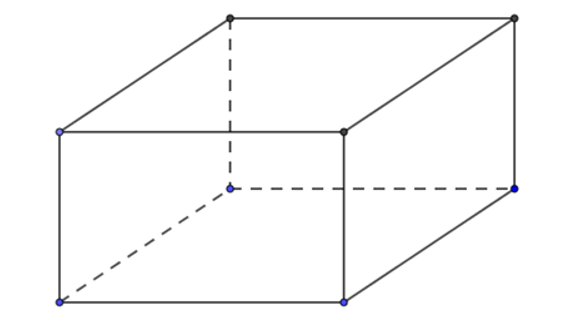
Gọi \(x,y\) lần lượt là chiều rộng và chiều dài của đáy hình hộp.
Điều kiện: \(x > 0;y > 0\left( m \right)\).
Ta có thể tích của khối hộp: \(V = 1xy = 400 \Rightarrow xy = 400 \Rightarrow y = \frac{{400}}{x}\left( {{m^3}} \right)\).
Diện tích mặt đáy: \({S_d} = xy = x.\frac{{400}}{x} = 400\left( {{{\rm{m}}^2}} \right)\).
Giá tiền để làm mặt đáy là: \(400.4000000 = {16.10^8}\) (đồng).
Diện tích xung quanh của bể cá: \({S_{xq}} = 2.x.1 + 2.y.1 = 2.\left( {x + y} \right) = 2.\left( {x + \frac{{400}}{x}} \right)\).
Giá tiền để làm mặt bên là: \(2.\left( {x + \frac{{400}}{x}} \right).3000000 = {6.10^6}.\left( {x + \frac{{400}}{x}} \right)\).
Tổng chi phí để xây dựng bể cá là:
\(T\left( x \right) = {6.10^6}.\left( {x + \frac{{400}}{x}} \right) + {24.10^8} \ge {6.10^6}.2\sqrt {x.\frac{{400}}{x}} + {24.10^8} \approx 2640{\rm{\;}}\) (triệu đồng).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.