Chọn cặp từ/ cụm từ thích hợp nhất điền vào chỗ trống.
Trước thách thức của thời gian, tốc độ đô thị hóa, đã có di tích trở thành _____, đặt ra nhiều yêu cầu với công tác _____ di sản hơn là việc chỉ đưa hình ảnh, video lên trang web.
Chọn cặp từ/ cụm từ thích hợp nhất điền vào chỗ trống.
Trước thách thức của thời gian, tốc độ đô thị hóa, đã có di tích trở thành _____, đặt ra nhiều yêu cầu với công tác _____ di sản hơn là việc chỉ đưa hình ảnh, video lên trang web.
Quảng cáo
Trả lời:
Đáp án đúng là B
Phương pháp giải
Căn cứ ngữ cảnh về nội dung câu văn.
Dạng bài điền từ
Lời giải
- Vị trí điền thứ nhất: vế đầu câu văn nói về thách thức của thời gian và đô thị hóa, thì những yếu tố này sẽ để lại thách thức tiêu cực -> từ “di sản” và “bảo vật” không phù hợp (loại A, D).
- Vị trí điền thứ hai: từ “bảo tồn” được hiểu là gìn giữ (cái có ý nghĩa lịch sử thuộc tài sản chung), không để bị mất mát, tổn thất -> rất hợp khi nói về việc gìn giữ các “di sản”; từ bảo vệ chỉ đơn thuần nói về việc chống lại sự hủy hoại, không phù hợp và chính xác khi đi kèm từ “di sản”.
=> Từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu văn trên là: phế tích/ bảo tồn.
Câu hoàn chỉnh: Trước thách thức của thời gian, tốc độ đô thị hóa, đã có di tích trở thành phế tích, đặt ra nhiều yêu cầu với công tác bảo tồn di sản hơn là việc chỉ đưa hình ảnh, video lên trang web.Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
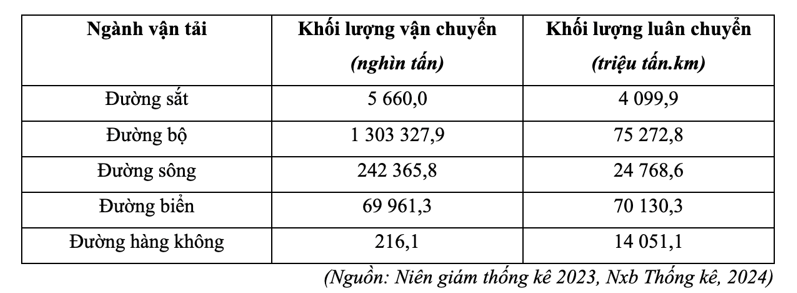
C. Đường sắt có cự li vận chuyển trung bình nhỏ hơn đường bộ.
Lời giải
Đáp án đúng là A
Phương pháp giải
Nhận xét bảng số liệu.
Lời giải
- Công thức:
Cự li vận chuyển trung bình = Khối lượng luân chuyển/Khối lượng vận chuyển.
- Dựa vào công thức tính trên, ta có bảng số liệu sau:
Cự li vận chuyển hàng hóa trung bình phân theo ngành vận tải của nước ta năm 2021
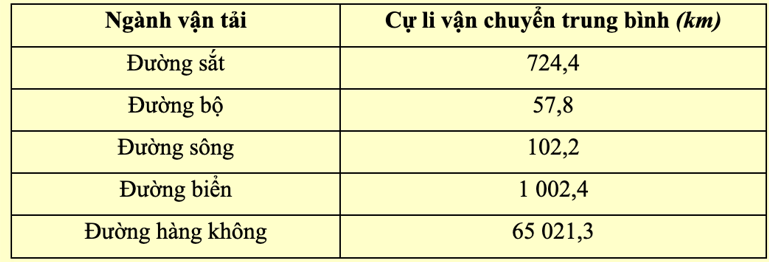
=> Đường hàng không có cự li vận chuyển trung bình dài nhất là nhận xét đúng.
Lời giải
Đáp án đúng là "2640"
Phương pháp giải
Tính giá trị nhỏ nhất
Lời giải
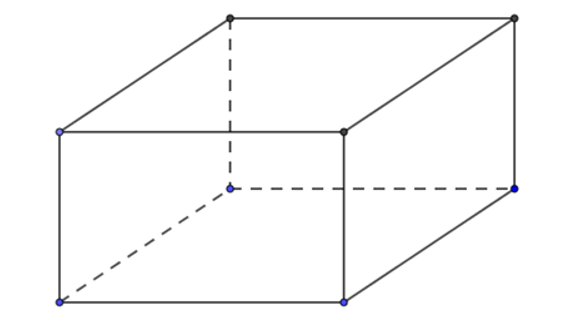
Gọi \(x,y\) lần lượt là chiều rộng và chiều dài của đáy hình hộp.
Điều kiện: \(x > 0;y > 0\left( m \right)\).
Ta có thể tích của khối hộp: \(V = 1xy = 400 \Rightarrow xy = 400 \Rightarrow y = \frac{{400}}{x}\left( {{m^3}} \right)\).
Diện tích mặt đáy: \({S_d} = xy = x.\frac{{400}}{x} = 400\left( {{{\rm{m}}^2}} \right)\).
Giá tiền để làm mặt đáy là: \(400.4000000 = {16.10^8}\) (đồng).
Diện tích xung quanh của bể cá: \({S_{xq}} = 2.x.1 + 2.y.1 = 2.\left( {x + y} \right) = 2.\left( {x + \frac{{400}}{x}} \right)\).
Giá tiền để làm mặt bên là: \(2.\left( {x + \frac{{400}}{x}} \right).3000000 = {6.10^6}.\left( {x + \frac{{400}}{x}} \right)\).
Tổng chi phí để xây dựng bể cá là:
\(T\left( x \right) = {6.10^6}.\left( {x + \frac{{400}}{x}} \right) + {24.10^8} \ge {6.10^6}.2\sqrt {x.\frac{{400}}{x}} + {24.10^8} \approx 2640{\rm{\;}}\) (triệu đồng).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.