Đọc đoạn trích và trả lời câu hỏi dưới đây.
Đời chúng ta đã nằm trong vòng chữ tôi. Mất bề rộng ta đi tìm bề sâu. Nhưng càng đi sâu càng lạnh. Ta thoát lên tiên cùng Thế Lữ, ta phiêu lưu trong trường tình cùng Lưu Trọng Lư, ta điên cuồng với Hàn Mặc Tử, Chế Lan Viên, ta đắm say cùng Xuân Diệu. Nhưng động tiên đã khép, tình yêu không bền, điên cuồng rồi tỉnh, say đắm vẫn bơ vơ. Ta ngơ ngẩn buồn trở về hồn ta cùng Huy Cận.
Cả trời thực, trời mộng vẫn nao nao theo hồn ta.
(Hoài Thanh - Hoài Chân, Thi nhân Việt Nam, NXB Văn học, Hà Nội, 2023)
Trong cụm từ “say đắm vẫn bơ vơ ”, Hoài Thanh chỉ nhà thơ nào?
Quảng cáo
Trả lời:
Đáp án đúng là B
Phương pháp giải
Căn cứ vào nội dung đoạn trích.
Dạng bài đọc hiểu văn bản văn học - Câu hỏi đơn
Lời giải
Trong đoạn văn, nhà phê bình Hoài Thanh đã sử dụng từ “đắm say” ở câu trước dành cho Xuân Diệu “ta đắm say cùng Xuân Diệu”. Đặc biệt xét đến phong cách nghệ thuật của Xuân Diệu có thể thấy vô cùng chính xác, thơ Xuân Diệu nồng nhiệt, đắm say tới vô cùng nhưng vì mặc cảm mà luôn không thoát khỏi sự lạc lõng, cô đơn, bơ vơ của một tâm hồn yêu đến điên dại.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
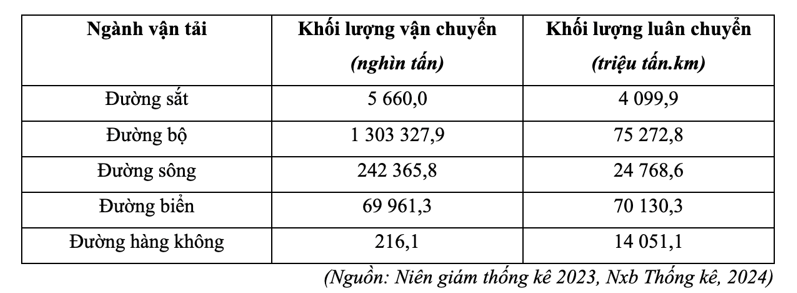
C. Đường sắt có cự li vận chuyển trung bình nhỏ hơn đường bộ.
Lời giải
Đáp án đúng là A
Phương pháp giải
Nhận xét bảng số liệu.
Lời giải
- Công thức:
Cự li vận chuyển trung bình = Khối lượng luân chuyển/Khối lượng vận chuyển.
- Dựa vào công thức tính trên, ta có bảng số liệu sau:
Cự li vận chuyển hàng hóa trung bình phân theo ngành vận tải của nước ta năm 2021
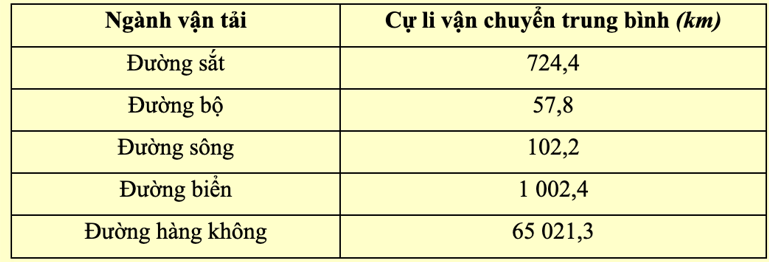
=> Đường hàng không có cự li vận chuyển trung bình dài nhất là nhận xét đúng.
Lời giải
Đáp án đúng là "2640"
Phương pháp giải
Tính giá trị nhỏ nhất
Lời giải
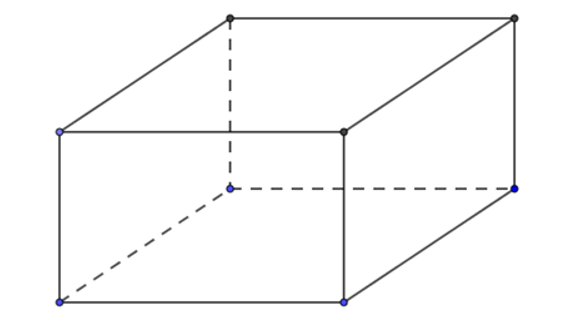
Gọi \(x,y\) lần lượt là chiều rộng và chiều dài của đáy hình hộp.
Điều kiện: \(x > 0;y > 0\left( m \right)\).
Ta có thể tích của khối hộp: \(V = 1xy = 400 \Rightarrow xy = 400 \Rightarrow y = \frac{{400}}{x}\left( {{m^3}} \right)\).
Diện tích mặt đáy: \({S_d} = xy = x.\frac{{400}}{x} = 400\left( {{{\rm{m}}^2}} \right)\).
Giá tiền để làm mặt đáy là: \(400.4000000 = {16.10^8}\) (đồng).
Diện tích xung quanh của bể cá: \({S_{xq}} = 2.x.1 + 2.y.1 = 2.\left( {x + y} \right) = 2.\left( {x + \frac{{400}}{x}} \right)\).
Giá tiền để làm mặt bên là: \(2.\left( {x + \frac{{400}}{x}} \right).3000000 = {6.10^6}.\left( {x + \frac{{400}}{x}} \right)\).
Tổng chi phí để xây dựng bể cá là:
\(T\left( x \right) = {6.10^6}.\left( {x + \frac{{400}}{x}} \right) + {24.10^8} \ge {6.10^6}.2\sqrt {x.\frac{{400}}{x}} + {24.10^8} \approx 2640{\rm{\;}}\) (triệu đồng).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.