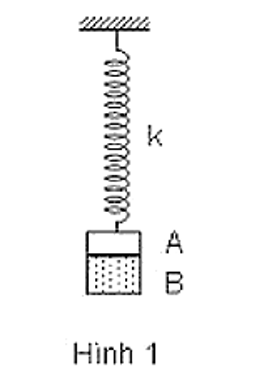
Hai vật A, B dán liền nhau mB = 2mA = 200g, treo vào một lò xo có độ cứng k = 50N/m, hình 1. Nâng vật lên đến đến vị trí lò xo có chiều dài tự nhiên l0 = 30cm thì buông nhẹ. Vật dao động điều hoà đến vị trí lực đàn hồi của lò xo có độ lớn lớn nhất, vật B bị tách ra. Tính chiều dài ngắn nhất của lò xo.
A. 26 cm.
B. 24 cm.
C. 30 cm.
D. 22 cm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là D
Phương pháp giải
Vận dụng lí thuyết về con lắc lò xo và chiều dài của con lắc trong quá trình dao động.
Áp dụng công thức tính độ biến dạng tại vị trí cân bằng.
Lời giải
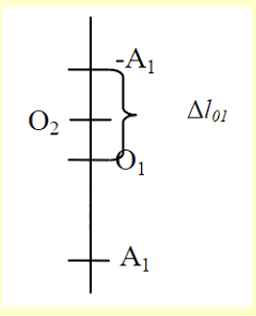
Khi B chưa rời khỏi A: \(\Delta {l_{01}} = \frac{{\left( {{m_A} + {m_B}} \right)g}}{k} = \frac{{(0,1 + 0,2).10}}{{50}} = 6\;{\rm{cm}}\)
Biên độ dao động của hệ khi B chưa rời khỏi A: \(A = \Delta {l_{01}} = 6\;{\rm{cm}}\)
Khi lò xo có lực đàn hồi max tức hai vật đang ở biên \({A_1}\) và \(v = 0\)
Khi B rời khỏi A . Hệ chỉ còn lò xo và vật A. Độ biến dạng tại VTCB mới \({O_2}\) là:
\(\Delta {l_{02}} = \frac{{{m_A}g}}{k} = \frac{{0,1.10}}{{50}} = 2\;{\rm{cm}}\)
Biên độ dao động mới: \({A_2} = 6 + (6 - 2) = 10\;{\rm{cm}}\)
Chiều dài cực tiểu: \({l_{\min }} = {l_0} + \Delta {l_{02}} - {A_2} = 22\;{\rm{cm}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Đường hàng không có cự li vận chuyển trung bình dài nhất.
B. Đường biển có cự li vận chuyển trung bình nhỏ hơn đường sông.
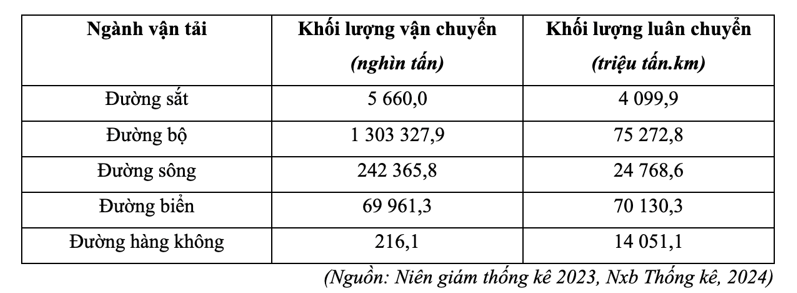
C. Đường sắt có cự li vận chuyển trung bình nhỏ hơn đường bộ.
D. Đường hàng không có cự li vận chuyển trung bình ngắn nhất.
Lời giải
Đáp án đúng là A
Phương pháp giải
Nhận xét bảng số liệu.
Lời giải
- Công thức:
Cự li vận chuyển trung bình = Khối lượng luân chuyển/Khối lượng vận chuyển.
- Dựa vào công thức tính trên, ta có bảng số liệu sau:
Cự li vận chuyển hàng hóa trung bình phân theo ngành vận tải của nước ta năm 2021
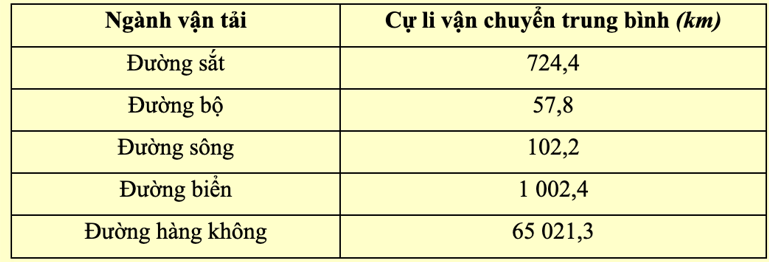
=> Đường hàng không có cự li vận chuyển trung bình dài nhất là nhận xét đúng.
Lời giải
Đáp án đúng là "2640"
Phương pháp giải
Tính giá trị nhỏ nhất
Lời giải
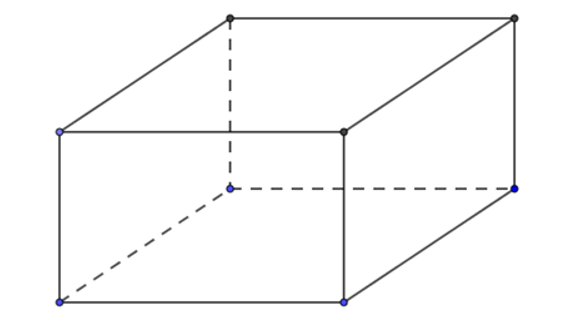
Gọi \(x,y\) lần lượt là chiều rộng và chiều dài của đáy hình hộp.
Điều kiện: \(x > 0;y > 0\left( m \right)\).
Ta có thể tích của khối hộp: \(V = 1xy = 400 \Rightarrow xy = 400 \Rightarrow y = \frac{{400}}{x}\left( {{m^3}} \right)\).
Diện tích mặt đáy: \({S_d} = xy = x.\frac{{400}}{x} = 400\left( {{{\rm{m}}^2}} \right)\).
Giá tiền để làm mặt đáy là: \(400.4000000 = {16.10^8}\) (đồng).
Diện tích xung quanh của bể cá: \({S_{xq}} = 2.x.1 + 2.y.1 = 2.\left( {x + y} \right) = 2.\left( {x + \frac{{400}}{x}} \right)\).
Giá tiền để làm mặt bên là: \(2.\left( {x + \frac{{400}}{x}} \right).3000000 = {6.10^6}.\left( {x + \frac{{400}}{x}} \right)\).
Tổng chi phí để xây dựng bể cá là:
\(T\left( x \right) = {6.10^6}.\left( {x + \frac{{400}}{x}} \right) + {24.10^8} \ge {6.10^6}.2\sqrt {x.\frac{{400}}{x}} + {24.10^8} \approx 2640{\rm{\;}}\) (triệu đồng).
Câu 3
A. 0Wb.
B. −5,196.10−4Wb.
C. −10,392.10−4Wb.
D. 10,392.10−4Wb.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{5}{{11}}\).
B. \(\frac{6}{{11}}\).
C. \(\frac{1}{2}\).
D. \(\frac{4}{{11}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. −1371 kJ/mol.
B. −954 kJ/mol.
C. −149 kJ/mol.
D. +149 kJ/mol.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập