Cho hình chóp \(S.ABCD\) có đáy là hình thang vuông tại A và D, hai mặt bên \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) đồng thời vuông góc với đáy. Biết \(AB = 2AD = 2CD = 2a\), khoảng cách từ A đến \(\left( {SBC} \right)\) bằng \(\frac{{\sqrt 6 }}{2}a\). Thể tích của khối chóp \(S.ABCD\) bằng:
Cho hình chóp \(S.ABCD\) có đáy là hình thang vuông tại A và D, hai mặt bên \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) đồng thời vuông góc với đáy. Biết \(AB = 2AD = 2CD = 2a\), khoảng cách từ A đến \(\left( {SBC} \right)\) bằng \(\frac{{\sqrt 6 }}{2}a\). Thể tích của khối chóp \(S.ABCD\) bằng:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là A
Phương pháp giải
Thể tích của khối chóp: \(V = \frac{1}{3}h.S\), trong đó \(h\) là chiều cao hình chóp, \(S\) là diện tích đáy của hình chóp
Lời giải
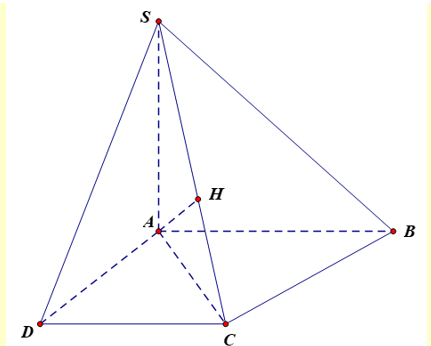
Ta có \(AB = 2AD = 2CD = 2a \Rightarrow AD = DC = a\)
Hai mặt bên \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) đồng thời vuông góc với đáy nên \(SA \bot \left( {ABCD} \right)\).
Dễ thấy \(\Delta ADC\) vuông cân tại \(D,\Delta ACB\) vuông cân tại \(C\) nên \(AC = AD\sqrt 2 = a\sqrt 2 \).
Gọi \(H\) là hình chiếu của \(A\) trên \(SC\). Khi đó \(AH \bot \left( {SCB} \right)\) nên \(AH = {d_{\left[ {A,\left( {SCB} \right)} \right]}} = \frac{{a\sqrt 6 }}{2}\).
Ta có
\(\frac{{{\rm{1\;}}}}{{A{H^2}}} = \frac{1}{{A{C^2}}} + \frac{1}{{S{A^2}}} \Rightarrow \frac{1}{{S{A^2}}} = \frac{1}{{A{H^2}}} - \frac{1}{{A{C^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 6 }}{2}} \right)}^2}}} - \frac{1}{{{{(a\sqrt 2 )}^2}}} \Rightarrow AH = a\sqrt 6 \)
Và \({S_{ABCD}} = \frac{{\left( {AB + DC} \right)AD}}{2} = \frac{{\left( {2a + a} \right)a}}{2} = \frac{{3{a^2}}}{2}\).
Thể tích của khối chóp \(S.ABCD\) là \({V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SA = \frac{1}{3}.\frac{{3{a^2}}}{2}.a\sqrt 6 = \frac{{{a^3}\sqrt 6 }}{2}\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là A
Phương pháp giải
Công suất hoạt động của tấm pin: \[P = IS\]
Sử dụng biểu thức tính nhiệt lượng: \[Q = mc{\rm{\Delta }}t\]
Vận dụng biểu thức tính hiệu suất.
Lời giải
Công suất hoạt động của 2 tấm thu năng lượng: \[P = IS = 1000.2.2.1,25 = 5000{\rm{W}}\]
Nhiệt lượng máy thu được trong t = 2h = 7200s là:
\[Q = H.P.{\rm{\Delta }}t = 0,96.5000.7200 = {3456.10^4}J\]
Mặt khác, ta có: \[Q = mc{\rm{\Delta }}t\]
⇒ Độ tăng nhiệt độ của 150kg nước khi máy hoạt động:
\[{\rm{\Delta }}T = \frac{Q}{{mc}} = \frac{{{{3456.10}^4}}}{{150.4180}} \approx {55^o}C\]
Câu 2
Lời giải
Đáp án đúng là C
Phương pháp giải
Giải bài toán bằng cách lập hệ phương trình.
Lời giải
Gọi \(x,y\left( {{\rm{kg}}} \right)\) lần lượt là khối lượng thanh long và nhãn chứa trong thùng 18 kg. Điều kiện\(0 \le x,y \le 18\)
Vi tổng khối lượng trái cây chứa trong thùng là 18 kg nên ta có phương trình \(x + y = 18\) (1)
Vì cái thùng có thể chứa tối đa 14 kg thanh long nên cứ 1 kg thanh long sẽ chiếm \(\frac{1}{{14}}\) thể tích cái thùng, do đó \(x\) kg thanh long sẽ chiếm \(\frac{x}{{14}}\) thể tích cái thùng.
Vì cái thùng có thể chứa tối đa 21 kg nhãn nên cứ 1 kg nhãn sẽ chiếm \(\frac{1}{{21}}\) thể tích cái thùng, do đó \(y{\rm{\;kg}}\) nhãn sẽ chiếm \(\frac{y}{{21}}\) thể tích cái thùng.
Vì người ta chứa đầy thùng đó bằng \(x{\rm{\;kg}}\) thanh long và \(y{\rm{\;kg}}\) nhãn nên ta có phương trình
\(\frac{x}{{14}} + \frac{y}{{21}} = 1\) (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y = 18}\\{\frac{x}{{14}} + \frac{y}{{21}} = 1}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 6}\\{y = 12}\end{array}} \right.} \right.\) (thỏa điều kiện).
Vậy khối lượng thanh long có trong thùng là 6 kg, khối lượng nhãn có trong thùng là 12 kg.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập