Cho hàm số \(y = \frac{{x + 4}}{{x - 3}}\). Điểm \(M\left( {{x_0};{y_0}} \right)\) (với \({y_0} > 0\)) thuộc đồ thị hàm số \(y = \frac{{x + 4}}{{x - 3}}\) sao cho tiếp tuyến tại \(M\) cắt các trục \[Ox,\,Oy\] lần lượt tại \(A\) và \(B\) thỏa mãn \(AB = 5 \cdot OA\sqrt 2 \). Tính giá trị của biểu thức \(T = 2{{\rm{x}}_0} + {y_0}\) (nhập đáp án vào ô trống).
Đáp án: ___
Quảng cáo
Trả lời:
Ta có: \(\Delta OAB\) vuông tại \(O\) ta có: \(\tan \widehat {BAO} = \frac{{OB}}{{OA}} = \frac{{\sqrt {A{B^2} - O{A^2}} }}{{OA}} = 7\).
Gọi \(k\) là hệ số góc của tiếp tuyến tại \(M\) của đồ thị hàm số \(y = \frac{{x + 4}}{{x - 3}}\), ta có: \(k = \pm 7\).
Ta có: \(y' = \frac{{ - 7}}{{{{\left( {x - 3} \right)}^2}}}\)\( \Rightarrow y'\left( {{x_0}} \right) = \frac{{ - 7}}{{{{\left( {{x_0} - 3} \right)}^2}}} = \pm 7 \Leftrightarrow {\left( {{x_0} - 3} \right)^2} = 1 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 4\\{x_0} = 2\end{array} \right.\).
Với \({x_0} = 4\) thì \({y_0} = \frac{{4 + 4}}{{4 - 3}} = 8\) > 0 (thỏa mãn). Suy ra \(M\left( {4;8} \right) \Rightarrow T = 16\).
Với \({x_0} = 2\) thì \({y_0} = \frac{{2 + 4}}{{2 - 3}} = - 6 < 0\) (loại).
Đáp án cần nhập là: \(16\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Tại \({t_0} = 70\) ta có: \(T\left( {70} \right) = 300\).
\(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ - }} \left( {20 + 4t} \right) = 300\); \(\mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} \left( {a - 2t} \right) = a - 140\).
Hàm số liên tục trên tập xác định khi: \(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = T\left( {70} \right)\)
\( \Leftrightarrow a - 140 = 300\)\( \Leftrightarrow a = 440\). Vậy giá trị của \(a = 440^\circ {\rm{C}}\). Chọn A.
Câu 2
Lời giải
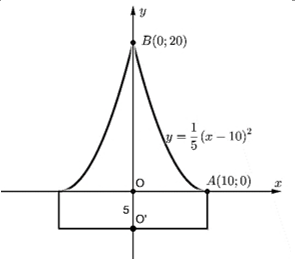
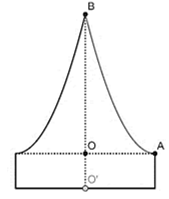
Chọn hệ trục tọa độ như hình vẽ bên.
Ta gọi thể tích của chiếc mũ là \(V\).
Thể tích của khối trụ có bán kính đáy bằng \(OA = 10\)cm và đường cao \(OO' = 5\)cm là \({V_1}\).
Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong \(AB\) và hai trục tọa độ quanh trục \(Oy\) là \({V_2}\). Khi đó, ta có \(V = {V_1} + {V_2}\).
Ta có \({V_1} = 5 \cdot {10^2}\pi = 500\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do parabol có đỉnh \(A\) nên nó có phương trình dạng \(\left( P \right):y = a{\left( {x - 10} \right)^2}\). Vì \(\left( P \right)\) qua điểm \(B\left( {0;20} \right)\) nên \(a = \frac{1}{5}\). Do đó, \(\left( P \right):y = \frac{1}{5}{\left( {x - 10} \right)^2}\). Từ đó suy ra \(x = 10 - \sqrt {5y} \) (do \(x < 10\)).
Suy ra \({V_2} = \pi \int\limits_0^{20} {{{\left( {10 - \sqrt {5y} } \right)}^2}{\rm{dy}}} = \pi \left( {3000 - \frac{{8000}}{3}} \right) = \frac{{1000}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do đó \(V = {V_1} + {V_2} = \frac{{1000}}{3}\pi + 500\pi = \frac{{2500}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
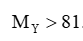 .
.