Elmon có 2024 hộp bánh quy, ban đầu tất cả hộp đều trống. Mỗi ngày, Elmon chọn hai hộp bánh phân biệt bất kì rồi cho vào mỗi hộp một chiếc bánh quy. Hằng đêm, Cookie Monster tìm đến hộp bánh có số bánh nhiều nhất và ăn toàn bộ số bánh trong hộp đó. Nếu quá trình này diễn ra vô hạn thì số bánh nhiều nhất mà Cookie Monster có thể ăn trong một buổi tối là bao nhiêu (nhập đáp án vào ô trống)?
Đáp án ___
Quảng cáo
Trả lời:
Giả sử hộp bánh thứ \(i\) chứa \({a_i}\) chiếc bánh quy, xét \(I = \sum\limits_{i = 1}^{2024} {\left\{ {\begin{array}{*{20}{l}}{{2^{{a_i}}},}&{{a_i} > 0}\\{0,}&{{a_i} = 0}\end{array}} \right.} \).
Nhận xét: Trước khi Elmon cho bánh vào hộp, ta luôn có \(I \le 4046\).
Chứng minh:
Giả sử \(I \le 4046\) và Elmon cho bánh quy vào các hộp chứa \(a\) và \(b\) chiếc bánh quy, trong đó \(a \le b\). Ta sẽ chứng minh sau khi Cookie Monster ăn bánh vào mỗi đêm, giá trị sau đó của \(I\), gọi là \(I'\)cũng thỏa mãn \(I' \le 4046\).
Nếu \(b > 0\), hành động của Elmon làm \(I\) tăng lên \({2^a} + {2^b}\), trong khi đó hành động của Cookie Monster làm \(I\) giảm ít nhất \({2^{b + 1}} \ge {2^b} + {2^a}\), do đó \(I' \le I \le 4046\).
Nếu \(a = b = 0\), hành động của Elmon làm \(I\) tăng lên 2, trong khi đó hành động của Cookie Monster làm \(I\) giảm ít nhất \(\frac{{I + 2}}{{2024}}\), do đó \(I' \le \frac{{2023}}{{2024}}\left( {I + 2} \right) \le 4046\).
Vậy trước khi Elmon hành động sẽ không có hộp bánh nào có ít nhất 12 chiếc bánh quy, do đó số bánh lớn nhất Cookie Monster có thể ăn là 12.
Xây dựng:
– Bằng cách chọn 1024 hộp bánh quy trống trong một hàng, Elmon có thể đảm bảo rằng mỗi hộp bánh trong 1024 hộp đều có 1 chiếc bánh quy.
– Bằng cách chọn 512 hộp bánh quy có 1 chiếc bánh trong mỗi lọ trong một hàng, Elmon có thể đảm bảo rằng mỗi hộp bánh trong 512 hộp đều có 2 chiếc bánh quy.
Tiếp tục quá trình trên, Elmon có thể đảm bảo rằng có \({2^{11 - n}}\) hộp bánh có \(n\) chiếc bánh ở mỗi hộp. Cuối cùng, Elmon có thể chắc chắn rằng có 1 hộp bánh chứa 11 chiếc bánh quy. Vào buổi đêm sau đó, Cookie Monster sẽ ăn 12 chiếc bánh quy.
Đáp án cần nhập là: \[12\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Tại \({t_0} = 70\) ta có: \(T\left( {70} \right) = 300\).
\(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ - }} \left( {20 + 4t} \right) = 300\); \(\mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} \left( {a - 2t} \right) = a - 140\).
Hàm số liên tục trên tập xác định khi: \(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = T\left( {70} \right)\)
\( \Leftrightarrow a - 140 = 300\)\( \Leftrightarrow a = 440\). Vậy giá trị của \(a = 440^\circ {\rm{C}}\). Chọn A.
Câu 2
Lời giải
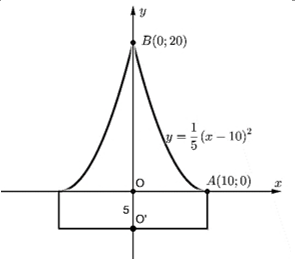
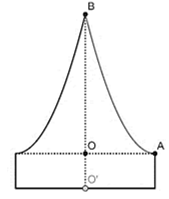
Chọn hệ trục tọa độ như hình vẽ bên.
Ta gọi thể tích của chiếc mũ là \(V\).
Thể tích của khối trụ có bán kính đáy bằng \(OA = 10\)cm và đường cao \(OO' = 5\)cm là \({V_1}\).
Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong \(AB\) và hai trục tọa độ quanh trục \(Oy\) là \({V_2}\). Khi đó, ta có \(V = {V_1} + {V_2}\).
Ta có \({V_1} = 5 \cdot {10^2}\pi = 500\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do parabol có đỉnh \(A\) nên nó có phương trình dạng \(\left( P \right):y = a{\left( {x - 10} \right)^2}\). Vì \(\left( P \right)\) qua điểm \(B\left( {0;20} \right)\) nên \(a = \frac{1}{5}\). Do đó, \(\left( P \right):y = \frac{1}{5}{\left( {x - 10} \right)^2}\). Từ đó suy ra \(x = 10 - \sqrt {5y} \) (do \(x < 10\)).
Suy ra \({V_2} = \pi \int\limits_0^{20} {{{\left( {10 - \sqrt {5y} } \right)}^2}{\rm{dy}}} = \pi \left( {3000 - \frac{{8000}}{3}} \right) = \frac{{1000}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do đó \(V = {V_1} + {V_2} = \frac{{1000}}{3}\pi + 500\pi = \frac{{2500}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
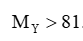 .
.