Cho hình sau:
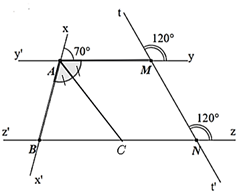
Biết \(\widehat {xAy} = 70^\circ ;\,\,\widehat {tMy} = 120^\circ ;\,\,\widehat {tNz} = 120^\circ \) và tia phân giác của \(\widehat {BAM}\) cắt đường thẳng \(zz'\) tại \(C\). Khi đó:
Cho hình sau:

Biết \(\widehat {xAy} = 70^\circ ;\,\,\widehat {tMy} = 120^\circ ;\,\,\widehat {tNz} = 120^\circ \) và tia phân giác của \(\widehat {BAM}\) cắt đường thẳng \(zz'\) tại \(C\). Khi đó:
a) \(yy'\parallel zz'\).
b) \(\widehat {ABN} = \widehat {xAM} = 70^\circ \) (hai góc so le trong).
c) \(\widehat {BAC} < \widehat {ABN}.\)
Quảng cáo
Trả lời:
a) Đúng.
Vì \[\widehat {tMy} = \widehat {MNz} = 120^\circ \] và hai góc ở vị trí đồng vị nên \(yy'\parallel zz'\).
b) Sai.
Vì \(yy'\parallel zz'\) nên \(\widehat {ABN} = \widehat {xAM} = 70^\circ \) (hai góc đồng vị).
c) Đúng.
Có \(\widehat {ABM} = 180^\circ - 70^\circ = 110^\circ \).
Vì \(AC\) là phân giác của \(\widehat {ABM}\) nên \(\widehat {BAC} = \widehat {CAM} = \frac{{110^\circ }}{2} = 55^\circ \).
Do đó, \(\widehat {BAC} < \widehat {ABN}\,\,\,\left( {55^\circ < 70^\circ } \right)\).
d) Đúng.
Có \(yy'\parallel zz'\) nên \(\widehat {MAC} = \widehat {ACB} = 55^\circ \) (so le trong).
Lại có \(\widehat {ACB}\) và \(\widehat {ACN}\) là hai góc kề bù nên \(\widehat {ACB} + \widehat {ACN} = 180^\circ \).
Suy ra \(\widehat {ACN} = 180^\circ - \widehat {ACB} = 180^\circ - 55^\circ = 125^\circ \)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
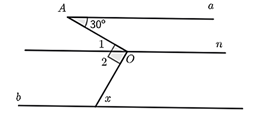
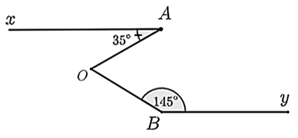
Ta có \(a\parallel n\) nên \(\widehat {aAn} = \widehat {{O_1}} = 30^\circ \) (so le trong)
Lại có, \(\widehat {{O_1}}\) và \(\widehat {{O_2}}\) là hai góc kề này nên \(\widehat {{O_1}} + \widehat {{O_2}} = \widehat {AOx}\) hay \(\widehat {{O_1}} + \widehat {{O_2}} = 90^\circ \).
Suy ra \(\widehat {{O_2}} = 90^\circ - \widehat {{O_1}} = 90^\circ - 30^\circ = 60^\circ \).
Vì \(n\parallel b\) nên \(x = \widehat {{O_2}} = 60^\circ \) (so le trong)
Câu 2
Lời giải
Đáp án đúng là: B
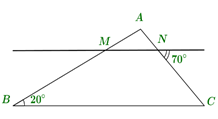
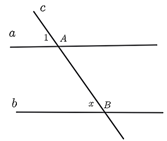
Do \(MN\,\parallel \,BC\) nên \(\widehat {\,AMN\,\,} = \widehat {B\;} = 20^\circ \) (hai góc đồng vị).
và \(\widehat {\,ANM\,\,} = 70^\circ \) (hai góc đối đỉnh).
Vậy \(\widehat {A\;} = 180^\circ - 20^\circ - 70^\circ = 90^\circ \).
Câu 3
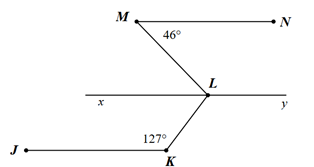
a) \[\widehat {KLx}\] và \[\widehat {xLM}\] là hai góc kề bù.
b) \[\widehat {NML} = \widehat {MLx} = 46^\circ \] (hai góc đồng vị).
c) \[\widehat {xLK} = 53^\circ \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
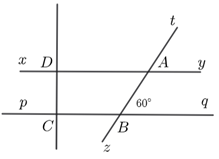
a) \[\widehat {xDC}\] và \[\widehat {DCB}\] là hai góc đồng vị.
b) \[\widehat {zBC}\] và \[\widehat {yAt}\] là hai góc đồng vị.
c) Hai đường thẳng \[xy\] và \[CD\] vuông góc với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
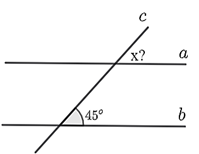
A. \(120^\circ .\)
B. \(60^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.