Ở một loài thực vật sinh sản bằng tự thụ phấn, gene A quy định khả năng nảy mầm trên đất có kim loại nặng, allele a không có khả năng này nên hạt có kiểu gene aa bị chết khi đất có kim loại nặng. Tiến hành gieo 1000 hạt (gồm 100 hạt AA, 400 hạt Aa, 500 hạt aa) trên đất có kim loại nặng các hạt sau khi nảy mầm đều sinh trưởng bình thường và các cây đều ra hoa, kết hạt tạo thế hệ F1; F1 nảy mầm và sinh trưởng, sau đó kết hạt tạo thế hệ F2. Lấy một hạt ở đời F2, xác suất để hạt nảy mầm được trên đất có kim loại nặng là bao nhiêu phần trăm (nhập đáp án vào ô trống)?
Đáp án ______
Quảng cáo
Trả lời:
- Ở thế hệ xuất phát, tỉ lệ kiểu gene ở cây trưởng thành là 0,2 AA : 0,8 Aa → Cho các cây trưởng thành ở thế hệ xuất phát tự thụ phấn (0,8 Aa tự thụ phấn sẽ sinh ra 3 loại kiểu gene là 0,2 AA : 0,4 AA : 0,2 aa; 0,2 AA tự thụ phấn sẽ sinh ra 0,2 AA) → Tỉ lệ hợp tử ở F1 là: 0,4 AA : 0,4 Aa : 0,2 aa.
- Vì hạt aa không nảy mầm được nên tỉ lệ kiểu gene ở cây trưởng thành F1 là: \(0,5AA:0,5Aa = \frac{1}{2}{\rm{AA}}:\frac{1}{2}{\rm{Aa}}\)→ Cho các cây trưởng thành ở thế hệ F1 tự thụ phấn → Tỉ lệ hợp tử ở F2 là: \(\frac{5}{8}{\rm{AA}}:\frac{1}{4}{\rm{Aa}}:\frac{1}{8}{\rm{aa}}\).
- Như vậy, ở F2 hạt nảy mầm gồm có \(\frac{5}{8}{\rm{AA}}\) và \(\frac{1}{4}{\rm{Aa}}\)→ Lấy ngẫu nhiên một hạt ở đời F2, xác suất để hạt này nảy mầm được trên đất có kim loại nặng là 5/8 + 1/4 = 87,5%. Đáp án: 87,5%.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Tại \({t_0} = 70\) ta có: \(T\left( {70} \right) = 300\).
\(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ - }} \left( {20 + 4t} \right) = 300\); \(\mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} \left( {a - 2t} \right) = a - 140\).
Hàm số liên tục trên tập xác định khi: \(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = T\left( {70} \right)\)
\( \Leftrightarrow a - 140 = 300\)\( \Leftrightarrow a = 440\). Vậy giá trị của \(a = 440^\circ {\rm{C}}\). Chọn A.
Câu 2
Lời giải
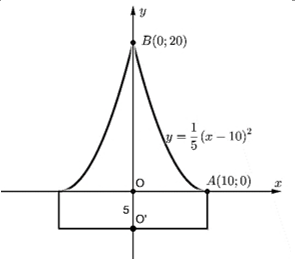
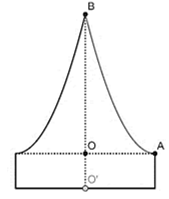
Chọn hệ trục tọa độ như hình vẽ bên.
Ta gọi thể tích của chiếc mũ là \(V\).
Thể tích của khối trụ có bán kính đáy bằng \(OA = 10\)cm và đường cao \(OO' = 5\)cm là \({V_1}\).
Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong \(AB\) và hai trục tọa độ quanh trục \(Oy\) là \({V_2}\). Khi đó, ta có \(V = {V_1} + {V_2}\).
Ta có \({V_1} = 5 \cdot {10^2}\pi = 500\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do parabol có đỉnh \(A\) nên nó có phương trình dạng \(\left( P \right):y = a{\left( {x - 10} \right)^2}\). Vì \(\left( P \right)\) qua điểm \(B\left( {0;20} \right)\) nên \(a = \frac{1}{5}\). Do đó, \(\left( P \right):y = \frac{1}{5}{\left( {x - 10} \right)^2}\). Từ đó suy ra \(x = 10 - \sqrt {5y} \) (do \(x < 10\)).
Suy ra \({V_2} = \pi \int\limits_0^{20} {{{\left( {10 - \sqrt {5y} } \right)}^2}{\rm{dy}}} = \pi \left( {3000 - \frac{{8000}}{3}} \right) = \frac{{1000}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do đó \(V = {V_1} + {V_2} = \frac{{1000}}{3}\pi + 500\pi = \frac{{2500}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
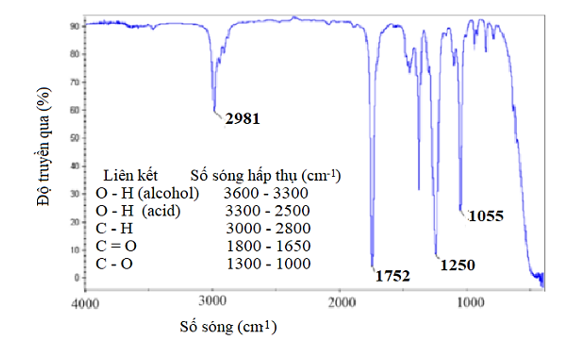
 .
.