Đọc đoạn thông tin sau và trả lời câu hỏi:
Thông tin. Lễ khao lề thế lính Hoàng Sa là nghi lễ “cúng thế lính” xưa của nhân dân các làng An Hải, An Vĩnh và các tộc họ trên đảo Lý Sơn (Quảng Ngãi) để cầu bình an cho người lính Hoàng Sa trước khi lên đường làm nhiệm vụ. Đây là một lễ thức dân gian được các tộc họ trên đảo Lý Sơn tổ chức vào khoảng tháng 2 và tháng 3 âm lịch hàng năm.
Hàng trăm năm trước, những người con ưu tú của quê hương Lý Sơn, tuân thủ lệnh vua đi ra Hoàng Sa, Trường Sa đo đạc hải trình, cắm mốc chủ quyền, khai thác sản vật. Nhiều người ra đi không trở về, thân xác họ đã hòa mình vào biển cả mênh mông.
Lễ khao lề thế lính Hoàng Sa trở thành một phong tục đẹp, một dấu ấn văn hóa tâm linh trong đời sống của các thế hệ người dân đảo Lý Sơn. Nghi lễ mang đậm tính nhân văn này đã được bảo tồn, duy trì suốt hơn 400 năm qua; tới Năm 2013, Lễ Khao lề thế lính Hoàng Sa được Bộ Văn hoá-Thể thao và Du lịch công nhận di sản văn hóa phi vật thể quốc gia.
Câu hỏi: Nhận định nào dưới đây không đúng về ý nghĩa của việc bảo tồn, duy trì Lễ Khao lề thế lính Hoàng Sa?
Đọc đoạn thông tin sau và trả lời câu hỏi:
|
Thông tin. Lễ khao lề thế lính Hoàng Sa là nghi lễ “cúng thế lính” xưa của nhân dân các làng An Hải, An Vĩnh và các tộc họ trên đảo Lý Sơn (Quảng Ngãi) để cầu bình an cho người lính Hoàng Sa trước khi lên đường làm nhiệm vụ. Đây là một lễ thức dân gian được các tộc họ trên đảo Lý Sơn tổ chức vào khoảng tháng 2 và tháng 3 âm lịch hàng năm. Hàng trăm năm trước, những người con ưu tú của quê hương Lý Sơn, tuân thủ lệnh vua đi ra Hoàng Sa, Trường Sa đo đạc hải trình, cắm mốc chủ quyền, khai thác sản vật. Nhiều người ra đi không trở về, thân xác họ đã hòa mình vào biển cả mênh mông. Lễ khao lề thế lính Hoàng Sa trở thành một phong tục đẹp, một dấu ấn văn hóa tâm linh trong đời sống của các thế hệ người dân đảo Lý Sơn. Nghi lễ mang đậm tính nhân văn này đã được bảo tồn, duy trì suốt hơn 400 năm qua; tới Năm 2013, Lễ Khao lề thế lính Hoàng Sa được Bộ Văn hoá-Thể thao và Du lịch công nhận di sản văn hóa phi vật thể quốc gia. |
Câu hỏi: Nhận định nào dưới đây không đúng về ý nghĩa của việc bảo tồn, duy trì Lễ Khao lề thế lính Hoàng Sa?
Quảng cáo
Trả lời:
Ý nghĩa của việc bảo tồn, duy trì Lễ Khao lề thế lính Hoàng Sa?
+ Tri ân công lao thế hệ đi trước trong việc xác lập, thực thi và bảo vệ chủ quyền biển đảo.
+ Tuyên truyền, giáo dục lòng yêu nước và ý thức bảo vệ chủ quyền biển, đảo của Tổ quốc.
+ Gìn giữ một cơ sở lịch sử để nhân dân Việt Nam đấu tranh bảo vệ chủ quyền biển, đảo.
→ Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Tại \({t_0} = 70\) ta có: \(T\left( {70} \right) = 300\).
\(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ - }} \left( {20 + 4t} \right) = 300\); \(\mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} \left( {a - 2t} \right) = a - 140\).
Hàm số liên tục trên tập xác định khi: \(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = T\left( {70} \right)\)
\( \Leftrightarrow a - 140 = 300\)\( \Leftrightarrow a = 440\). Vậy giá trị của \(a = 440^\circ {\rm{C}}\). Chọn A.
Câu 2
Lời giải
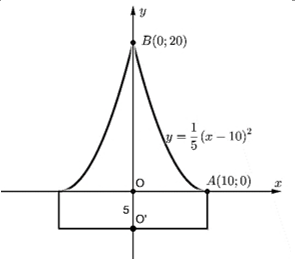
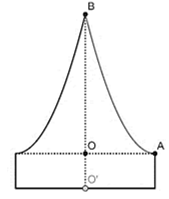
Chọn hệ trục tọa độ như hình vẽ bên.
Ta gọi thể tích của chiếc mũ là \(V\).
Thể tích của khối trụ có bán kính đáy bằng \(OA = 10\)cm và đường cao \(OO' = 5\)cm là \({V_1}\).
Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong \(AB\) và hai trục tọa độ quanh trục \(Oy\) là \({V_2}\). Khi đó, ta có \(V = {V_1} + {V_2}\).
Ta có \({V_1} = 5 \cdot {10^2}\pi = 500\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do parabol có đỉnh \(A\) nên nó có phương trình dạng \(\left( P \right):y = a{\left( {x - 10} \right)^2}\). Vì \(\left( P \right)\) qua điểm \(B\left( {0;20} \right)\) nên \(a = \frac{1}{5}\). Do đó, \(\left( P \right):y = \frac{1}{5}{\left( {x - 10} \right)^2}\). Từ đó suy ra \(x = 10 - \sqrt {5y} \) (do \(x < 10\)).
Suy ra \({V_2} = \pi \int\limits_0^{20} {{{\left( {10 - \sqrt {5y} } \right)}^2}{\rm{dy}}} = \pi \left( {3000 - \frac{{8000}}{3}} \right) = \frac{{1000}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do đó \(V = {V_1} + {V_2} = \frac{{1000}}{3}\pi + 500\pi = \frac{{2500}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
 .
.