They did not have access to education. It restricted their ability to reach their career targets.
They did not have access to education. It restricted their ability to reach their career targets.
Quảng cáo
Trả lời:
Kiến thức về câu chẻ
Dịch: Họ không được đi học. Điều này hạn chế khả năng đạt được mục tiêu nghề nghiệp của họ.
A. Họ có thể vượt qua hạn chế về cơ hội nghề nghiệp khi họ được đi học.
→ Sai nghĩa. Ngược nghĩa với câu gốc.
B. Rõ ràng là việc được đi học đã giúp họ đạt được ước mơ nghề nghiệp của mình.
→ Sai nghĩa. Ngược nghĩa với câu gốc.
C. Nếu họ được đi học, họ sẽ có thể hướng tới mục tiêu nghề nghiệp của mình.
→ Sai nghĩa. Câu điều kiện loại 2: If + S + V (QKĐ) + O, S + would/could/should + V-inf + O: Dùng để diễn tả tình huống, hành động không có thật và không thể xảy ra ở hiện tại và tương lai.
D. Chính việc không được đi học đã cản trở khả năng đạt được mục tiêu nghề nghiệp của họ.
→ Đúng. Cấu trúc câu chẻ nhấn mạnh chủ ngữ: It + is/was + chủ ngữ nhấn mạnh + who/that + V + O.
Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Tại \({t_0} = 70\) ta có: \(T\left( {70} \right) = 300\).
\(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ - }} \left( {20 + 4t} \right) = 300\); \(\mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} \left( {a - 2t} \right) = a - 140\).
Hàm số liên tục trên tập xác định khi: \(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = T\left( {70} \right)\)
\( \Leftrightarrow a - 140 = 300\)\( \Leftrightarrow a = 440\). Vậy giá trị của \(a = 440^\circ {\rm{C}}\). Chọn A.
Câu 2
Lời giải
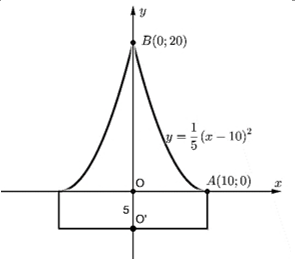
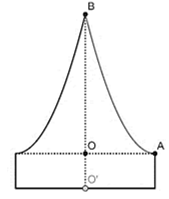
Chọn hệ trục tọa độ như hình vẽ bên.
Ta gọi thể tích của chiếc mũ là \(V\).
Thể tích của khối trụ có bán kính đáy bằng \(OA = 10\)cm và đường cao \(OO' = 5\)cm là \({V_1}\).
Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong \(AB\) và hai trục tọa độ quanh trục \(Oy\) là \({V_2}\). Khi đó, ta có \(V = {V_1} + {V_2}\).
Ta có \({V_1} = 5 \cdot {10^2}\pi = 500\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do parabol có đỉnh \(A\) nên nó có phương trình dạng \(\left( P \right):y = a{\left( {x - 10} \right)^2}\). Vì \(\left( P \right)\) qua điểm \(B\left( {0;20} \right)\) nên \(a = \frac{1}{5}\). Do đó, \(\left( P \right):y = \frac{1}{5}{\left( {x - 10} \right)^2}\). Từ đó suy ra \(x = 10 - \sqrt {5y} \) (do \(x < 10\)).
Suy ra \({V_2} = \pi \int\limits_0^{20} {{{\left( {10 - \sqrt {5y} } \right)}^2}{\rm{dy}}} = \pi \left( {3000 - \frac{{8000}}{3}} \right) = \frac{{1000}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do đó \(V = {V_1} + {V_2} = \frac{{1000}}{3}\pi + 500\pi = \frac{{2500}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
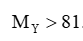 .
.