Which of the following situations best exemplifies “compensation” where someone makes up for a loss or damage they caused?
Which of the following situations best exemplifies “compensation” where someone makes up for a loss or damage they caused?
Quảng cáo
Trả lời:
Kiến thức về nghĩa của từ, suy luận
Trong các tình huống sau đây, tình huống nào minh họa rõ nhất cho từ “bồi thường” khi ai đó bù đắp cho mất mát hoặc thiệt hại mà họ gây ra?
A. Sarah quên trả lại chiếc áo khoác mượn của bạn đúng hạn. Cô ấy xin lỗi và đảm bảo với bạn rằng cô ấy sẽ trả lại vào ngày hôm sau.
B. Sarah vô tình làm đổ nước trái cây lên cuốn sách yêu thích của bạn mình. Cô ấy mời bạn mình đi uống cà phê và tặng anh ấy một cuốn sách mới.
C. Sarah làm vỡ một chiếc đĩa khi rửa bát tại nhà bạn mình. Cô ấy dành thời gian để cẩn thận dọn dẹp đống bừa bộn và chân thành xin lỗi.
D. Sarah mượn xe đạp của bạn mình và trả lại với chiếc lốp xẹp. Cô ấy hứa sẽ trả lại xe đạp ngay sau khi tự mình vá lốp.
→ Hành động bồi thường khi làm hư hại đồ vật của ai đó.
Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Tại \({t_0} = 70\) ta có: \(T\left( {70} \right) = 300\).
\(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ - }} \left( {20 + 4t} \right) = 300\); \(\mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} \left( {a - 2t} \right) = a - 140\).
Hàm số liên tục trên tập xác định khi: \(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = T\left( {70} \right)\)
\( \Leftrightarrow a - 140 = 300\)\( \Leftrightarrow a = 440\). Vậy giá trị của \(a = 440^\circ {\rm{C}}\). Chọn A.
Câu 2
Lời giải
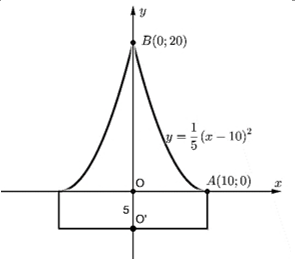
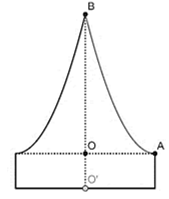
Chọn hệ trục tọa độ như hình vẽ bên.
Ta gọi thể tích của chiếc mũ là \(V\).
Thể tích của khối trụ có bán kính đáy bằng \(OA = 10\)cm và đường cao \(OO' = 5\)cm là \({V_1}\).
Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong \(AB\) và hai trục tọa độ quanh trục \(Oy\) là \({V_2}\). Khi đó, ta có \(V = {V_1} + {V_2}\).
Ta có \({V_1} = 5 \cdot {10^2}\pi = 500\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do parabol có đỉnh \(A\) nên nó có phương trình dạng \(\left( P \right):y = a{\left( {x - 10} \right)^2}\). Vì \(\left( P \right)\) qua điểm \(B\left( {0;20} \right)\) nên \(a = \frac{1}{5}\). Do đó, \(\left( P \right):y = \frac{1}{5}{\left( {x - 10} \right)^2}\). Từ đó suy ra \(x = 10 - \sqrt {5y} \) (do \(x < 10\)).
Suy ra \({V_2} = \pi \int\limits_0^{20} {{{\left( {10 - \sqrt {5y} } \right)}^2}{\rm{dy}}} = \pi \left( {3000 - \frac{{8000}}{3}} \right) = \frac{{1000}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do đó \(V = {V_1} + {V_2} = \frac{{1000}}{3}\pi + 500\pi = \frac{{2500}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
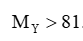 .
.