1) Hải đăng Kê Gà thuộc xã Tân Thành, Lâm Đồng là ngọn hải đăng được trung tâm sách kỷ luật Việt Nam xác nhận là ngọn hải đăng cao nhất và nhiều tuổi nhất. Hải đăng Kê Gà được xây dựng từ năm 1897-1899 và toàn bộ bằng đá. Tháp đèn có hình bát giác, cao \(66\,\,{\rm{m}}\) so với mực nước biển. Ngọn đèn đặt trong tháp có thể phát sáng xa 22 hải lý (tương đương \(40\,\,{\rm{km}}\,{\rm{)}}{\rm{.}}\)
Một người đi thuyền thúng trên biển, muốn đến ngọn hải đăng có độ cao \(66\,\,{\rm{m}}\,{\rm{,}}\) người đó đứng trên mũi thuyền và dùng giác kế đo được góc giữa thuyền và tia nắng chiều từ đỉnh ngọn hải đăng đến thuyền là \(36^\circ .\) Tính khoảng cách của thuyền đến ngọn hải đăng (làm tròn đến hàng phần trăm).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hình vẽ minh họa bài toán.
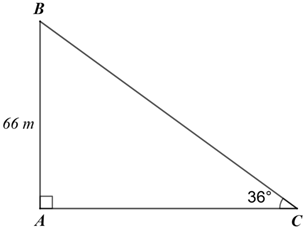
Độ cao của ngọn hải đăng là \(AB = 66\,\,{\rm{m}}\,{\rm{;}}\)
Góc giữa thuyền và tia nắng chiều từ đỉnh ngọn hải đăng đến thuyền là \(\widehat C = 36^\circ .\)
Xét \[\Delta ABC\] vuông tại \[A,\] ta có: \(\tan C = \frac{{AB}}{{AC}}\) (tỉ số lượng giác của góc nhọn).
Suy ra \(AC = \frac{{AB}}{{\tan C}} = \frac{{66}}{{\tan 36^\circ }} \approx 90,84\,\,({\rm{m}}).\)
Vậy khoảng cách của thuyền đến ngọn hải đăng khoảng \(90,84\,\,{\rm{m}}\,.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) và \(y\) (chiếc xe) lần lượt là số xe 35 chỗ ngồi và 50 chỗ ngồi \(\left( {x,\,\,y \in \mathbb{N}} \right).\)
Theo đề bài, ta có: \(35x + 50y = 645\) hay \(7x + 10y = 129.\)
Vì \(10y\) là số chẵn nên \(7x\) phải là số lẻ suy ra \(x\) là số lẻ.
Mặt khác \(7x \le 129\) suy ra \(x \le 18.\)
Do đó \(x \in \left\{ {1\,;\,\,3\,;\,\,5\,;\,\,7\,;\,\,9\,;\,\,11\,;\,\,13\,;\,\,15\,;\,\,17} \right\}.\)
Từ \(7x + 10y = 129\) nên \(y = \frac{{129 - 7x}}{{10}}.\)
Ta có bảng sau:
|
\(x\) |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
|
\(y\) |
\[12,2\] |
\[10,8\] |
\[9,4\] |
8 |
\(6,6\) |
\(5,2\) |
\(3,8\) |
\(2,4\) |
1 |
Vì \(x,\,\,y \in \mathbb{N}\) nên số chiếc xe để vừa đủ số chỗ ngồi cho 645 người thì \(\left( {x\,;\,\,y} \right) \in \left\{ {\left( {7\,;\,\,8} \right)\,;\,\,\left( {17\,;\,\,1} \right)} \right\}.\)
Tổng chi phí thuê xe là: \(C = 3\,\,500\,\,000x + 5\,\,200\,\,000y\) (đồng).
• Với thì \(C = 3\,\,500\,\,000 \cdot 7 + 5\,\,200\,\,000 \cdot 8 = 66\,\,100\,\,000\) (đồng).
• Với thì \(C = 3\,\,500\,\,000 \cdot 17 + 5\,\,200\,\,000 \cdot 1 = 64\,\,700\,\,000\) (đồng).
Ta thấy \(64\,\,700\,\,000 < 66\,\,100\,\,000\).
Do đó, nhà trường cần thuê 17 chiếc xe chỗ ngồi và 1 chiếc xe 50 chỗ ngồi để vừa đủ số chỗ ngồi cho 645 người và chi phí thuê xe là ít nhất
Lời giải
1) Gọi vận tốc ô tô là x (km/h), x > 20
Vận tốc xe máy là x – 20 (km/h)
Thời gian đi của ô tô là: \(\frac{{120}}{x}\) (h)
Thời gian đi của xe máy là: \(\frac{{120}}{{x - 20}}\) (h)
Vì xe máy đến B muộn hơn xe ô tô là 1 giờ nên ta có phương trình: \(\frac{{120}}{{x - 20}} - \frac{{120}}{x} = 1\)
Hay: \({x^2} - 20x - 2400 = 0\)
Nên \(\left( {x - 60} \right)\left( {x + 40} \right) = 0\)
Ta được \(x = 60(TM);\,x = - 40(KTM)\)
Vậy vận tốc của ô tô là 60km/h; vận tốc của xe máy là 40km/h
2) Gọi số tiền tiết kiệm mà chị Ngân gửi là x (đồng), x > 0
Tiền lãi chị Ngân nhận được sau 12 tháng là: \(6,2\% x\)( đồng)
Tổng số tiền chị Ngân nhận được sau khi gửi 12 tháng là \(x + 6,2\% x = 106,2\% x\)(đồng)
Chị Ngân dự định tổng số tiền nhận được sau khi gửi 12 tháng ít nhất là 318 600 000 đồng nên ta có bất phương trình:
\(106,2\% x \ge 318600000\)
\(x \ge 300000000\)
Vì x nhỏ nhất nên \(x = 300000000\)
Vậy chị Ngân phải gửi số tiền tiết kiệm ít nhất là 300 000 000 đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập