Một trường THCS dự định tổ chức cho 645 người gồm giáo viên và học sinh hai khối 8 và 9 tham gia hoạt động trải nghiệm. Nhà trường đã liên hệ với công ty du lịch để thuê 2 loại xe. Loại xe 35 chỗ ngồi và loại xe 50 chỗ ngồi (không kể lái xe). Biết rằng giá thuê xe loại 35 chỗ ngồi là \(3\,\,500\,\,000\) đồng/chiếc; loại xe 50 chỗ ngồi là \(5\,\,200\,\,000\) đồng/chiếc. Hỏi nhà trường cần thuê mỗi loại bao nhiêu chiếc để vừa đủ số chỗ ngồi cho 645 người và chi phí thuê xe là ít nhất?
Một trường THCS dự định tổ chức cho 645 người gồm giáo viên và học sinh hai khối 8 và 9 tham gia hoạt động trải nghiệm. Nhà trường đã liên hệ với công ty du lịch để thuê 2 loại xe. Loại xe 35 chỗ ngồi và loại xe 50 chỗ ngồi (không kể lái xe). Biết rằng giá thuê xe loại 35 chỗ ngồi là \(3\,\,500\,\,000\) đồng/chiếc; loại xe 50 chỗ ngồi là \(5\,\,200\,\,000\) đồng/chiếc. Hỏi nhà trường cần thuê mỗi loại bao nhiêu chiếc để vừa đủ số chỗ ngồi cho 645 người và chi phí thuê xe là ít nhất?
Quảng cáo
Trả lời:
Gọi \(x\) và \(y\) (chiếc xe) lần lượt là số xe 35 chỗ ngồi và 50 chỗ ngồi \(\left( {x,\,\,y \in \mathbb{N}} \right).\)
Theo đề bài, ta có: \(35x + 50y = 645\) hay \(7x + 10y = 129.\)
Vì \(10y\) là số chẵn nên \(7x\) phải là số lẻ suy ra \(x\) là số lẻ.
Mặt khác \(7x \le 129\) suy ra \(x \le 18.\)
Do đó \(x \in \left\{ {1\,;\,\,3\,;\,\,5\,;\,\,7\,;\,\,9\,;\,\,11\,;\,\,13\,;\,\,15\,;\,\,17} \right\}.\)
Từ \(7x + 10y = 129\) nên \(y = \frac{{129 - 7x}}{{10}}.\)
Ta có bảng sau:
|
\(x\) |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
|
\(y\) |
\[12,2\] |
\[10,8\] |
\[9,4\] |
8 |
\(6,6\) |
\(5,2\) |
\(3,8\) |
\(2,4\) |
1 |
Vì \(x,\,\,y \in \mathbb{N}\) nên số chiếc xe để vừa đủ số chỗ ngồi cho 645 người thì \(\left( {x\,;\,\,y} \right) \in \left\{ {\left( {7\,;\,\,8} \right)\,;\,\,\left( {17\,;\,\,1} \right)} \right\}.\)
Tổng chi phí thuê xe là: \(C = 3\,\,500\,\,000x + 5\,\,200\,\,000y\) (đồng).
• Với thì \(C = 3\,\,500\,\,000 \cdot 7 + 5\,\,200\,\,000 \cdot 8 = 66\,\,100\,\,000\) (đồng).
• Với thì \(C = 3\,\,500\,\,000 \cdot 17 + 5\,\,200\,\,000 \cdot 1 = 64\,\,700\,\,000\) (đồng).
Ta thấy \(64\,\,700\,\,000 < 66\,\,100\,\,000\).
Do đó, nhà trường cần thuê 17 chiếc xe chỗ ngồi và 1 chiếc xe 50 chỗ ngồi để vừa đủ số chỗ ngồi cho 645 người và chi phí thuê xe là ít nhất
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1) Gọi vận tốc ô tô là x (km/h), x > 20
Vận tốc xe máy là x – 20 (km/h)
Thời gian đi của ô tô là: \(\frac{{120}}{x}\) (h)
Thời gian đi của xe máy là: \(\frac{{120}}{{x - 20}}\) (h)
Vì xe máy đến B muộn hơn xe ô tô là 1 giờ nên ta có phương trình: \(\frac{{120}}{{x - 20}} - \frac{{120}}{x} = 1\)
Hay: \({x^2} - 20x - 2400 = 0\)
Nên \(\left( {x - 60} \right)\left( {x + 40} \right) = 0\)
Ta được \(x = 60(TM);\,x = - 40(KTM)\)
Vậy vận tốc của ô tô là 60km/h; vận tốc của xe máy là 40km/h
2) Gọi số tiền tiết kiệm mà chị Ngân gửi là x (đồng), x > 0
Tiền lãi chị Ngân nhận được sau 12 tháng là: \(6,2\% x\)( đồng)
Tổng số tiền chị Ngân nhận được sau khi gửi 12 tháng là \(x + 6,2\% x = 106,2\% x\)(đồng)
Chị Ngân dự định tổng số tiền nhận được sau khi gửi 12 tháng ít nhất là 318 600 000 đồng nên ta có bất phương trình:
\(106,2\% x \ge 318600000\)
\(x \ge 300000000\)
Vì x nhỏ nhất nên \(x = 300000000\)
Vậy chị Ngân phải gửi số tiền tiết kiệm ít nhất là 300 000 000 đồng.
Lời giải
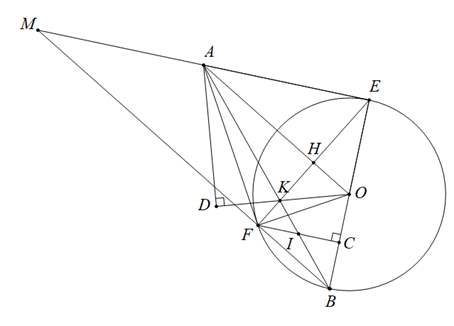
a) Vì \[AD \bot DO\] (gt) nên \[\widehat {ADO} = 90^\circ \], khi đó \[\Delta ADO\] vuông tại \[D\]
Vì \[\Delta ADO\] vuông tại \[D\] nên ba điểm \[A,D,O\] cùng thuộc đường tròn đường kính \[AO\] (1)
Vì \[AE\] là tiếp tuyến của \[\left( O \right)\] nên \[AE \bot OE\], do đó \[\widehat {AEO} = 90^\circ \], khi đó \[\Delta AEO\] vuông tại \[E\]
Vì \[\Delta AEO\] vuông tại \[E\] nên ba điểm \[A,E,O\] cùng thuộc đường tròn đường kính \[AO\] (2)
Từ (1), (2) suy ra bốn điểm \(D,A,E,O\) cùng thuộc một đường tròn.
b) Xét \[\Delta AEO\] và \[\Delta AFO\] có:
\[EO = FO\left( { = R} \right)\]
\[\widehat {EOA} = \widehat {FOA}\] (gt)
\[AO\] chung
Do đó \[\Delta AEO = \Delta AFO\] (c.g.c)
Suy ra \[\widehat {AFO} = \widehat {AEO}\] (hai góc tương ứng)
Mà \[\widehat {AEO} = 90^\circ \] nên \[\widehat {AFO} = 90^\circ \]
Xét \[\left( O \right)\] có \[AF \bot FO\] tại \[F \in \left( O \right)\] nên \[AF\] là tiếp tuyến của \[\left( O \right)\] tại tiếp điểm \(F\).
Vì \[OE = OF\] nên \[O\] thuộc đường trung trực của \[FE\]
Vì \[AF = AE\]nên \[A\] thuộc đường trung trực của \[FE\]
Do đó \[AO\] là đường trung trực \[FE\].
Suy ra \[AO \bot FE\] tại \[H\]
Xét \[\Delta OHK\] và \[\Delta ODA\] có:
\[\widehat {AOD}\] chung
\[\widehat {OHK} = \widehat {ODA} = 90^\circ \]
Do đó (g.g)
Suy ra \[\frac{{OK}}{{OA}} = \frac{{OH}}{{OD}}\], khi đó \[OK.OD = OH.OA\]
c) Gọi \(M\) là giao điểm của \(BF;AE\).
\(\Delta BFE\) có \(OB = OE = FO = \frac{{BE}}{2}\) nên \(\Delta BFE\) vuông tại \(F\).
Suy ra \(BM \bot FE\) mà \[AO \bot FE\] nên \(AO\,{\rm{//}}\,BM\)
\(\Delta BEM\) có \(AO\,{\rm{//}}\,BM\) và \(O\) là trung điểm của \(BE\) nên \(A\) là trung điểm của \(EM\) hay \(AM = AE\)
Có \(AE \bot BE;FC \bot BE \Rightarrow AE\,{\rm{//}}\,FC\)
Vì \(AE\,{\rm{//}}\,FC\) nên theo định lí Thalès ta có: \(\frac{{IC}}{{AE}} = \frac{{BI}}{{BA}}\) và \[\frac{{FI}}{{AM}} = \frac{{BI}}{{BA}}\]
Nên \(\frac{{IC}}{{AE}} = \frac{{FI}}{{AM}}\) mà \(AM = AE\) nên \(IC = FI\) hay \[I\] là trung điểm của \[FC\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.