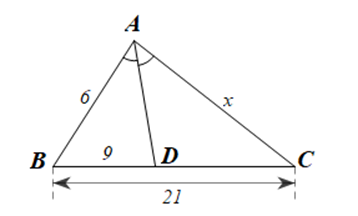
1) Cho \(\Delta ABC.\) Tia phân giác góc trong của góc \[A\] cắt \[BC\] tại \[D.\] Cho \[AB = 6,\] \[AC = x,\] \[BD = 9,\] \[BC = 21.\] Tìm \(x.\)
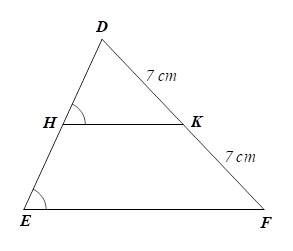
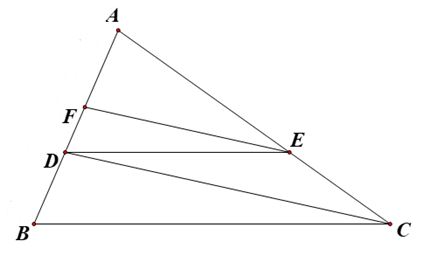
2) Cho tam giác \[ABC,\] các đường trung tuyến \[BD,{\rm{ }}CE.\] Gọi \[M,{\rm{ }}N\] theo thứ tự là trung điểm của \[BE,{\rm{ }}CD.\] Gọi \[I,{\rm{ }}K\] theo thứ tự là giao điểm của \[MN\] với \[BD\] và \[CE.\] Chứng minh rằng:
a) \[ED\,{\rm{//}}\,BC.\] b) \[MN\,{\rm{//}}\,BC.\] c) \[MI = IK = KN.\]
1) Cho \(\Delta ABC.\) Tia phân giác góc trong của góc \[A\] cắt \[BC\] tại \[D.\] Cho \[AB = 6,\] \[AC = x,\] \[BD = 9,\] \[BC = 21.\] Tìm \(x.\)
2) Cho tam giác \[ABC,\] các đường trung tuyến \[BD,{\rm{ }}CE.\] Gọi \[M,{\rm{ }}N\] theo thứ tự là trung điểm của \[BE,{\rm{ }}CD.\] Gọi \[I,{\rm{ }}K\] theo thứ tự là giao điểm của \[MN\] với \[BD\] và \[CE.\] Chứng minh rằng:
a) \[ED\,{\rm{//}}\,BC.\] b) \[MN\,{\rm{//}}\,BC.\] c) \[MI = IK = KN.\]
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
|
1) Ta có: \[BC = BD + DC\] nên \[DC = BC - BD = 21 - 9{\rm{ }} = 12.\] Trong \(\Delta ABC,\) \[AD\] là phân giác của \(\widehat {BAC}\) nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\) (tính chất đường phân giác của tam giác) Hay \(\frac{6}{x} = \frac{9}{{12}}\), suy ra \(x = \frac{{6 \cdot 12}}{9} = 8.\)
|
 |
|
2) a) Trong \(\Delta ABC\) có các đường trung tuyến \[BD,{\rm{ }}CE\] nên \[D\] là trung điểm của \[AC,\] \[E\] là trung điểm của \[AB\] nên \[ED\] là đường trung bình của \(\Delta ABC.\) Suy ra \(ED = \frac{1}{2}BC\) và \[ED\,{\rm{//}}\,BC\] (tính chất đường trung bình của tam giác). |
 |
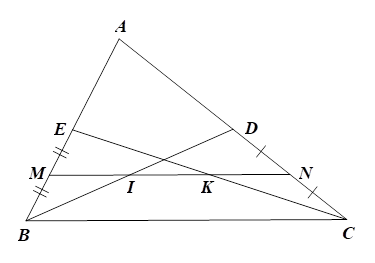b) Ta có: \[E\] là trung điểm của \[AB\] nên \(AE = EB = \frac{1}{2}AB.\)
Mà \[M\] là trung điểm của \[EB\] nên \(EM = MB = \frac{1}{2}EB = \frac{1}{4}AB\) hay \(\frac{{MB}}{{AB}} = \frac{1}{4}.\)
Tương tự, ta cũng có \(NC = \frac{1}{4}AC\) hay \(\frac{{NC}}{{AC}} = \frac{1}{4}.\)
Suy ra \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\,\,\left( { = \frac{1}{4}} \right).\)
Xét \(\Delta ABC\) có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) nên \[MN\,{\rm{//}}\,BC\] (định lí Thalès đảo).
c) Ta có \[MN\,{\rm{//}}\,BC\] (câu b) và \[ED\,{\rm{//}}\,BC\] (câu a) nên \[ED\,{\rm{//}}\,MN\,{\rm{//}}\,BC.\]
Xét \(\Delta BDE\) có \[M\] là trung điểm của \[EB\] và \[MI\,{\rm{//}}\,ED\] (do \[ED\,{\rm{//}}\,MN)\]
Suy ra \[I\] là trung điểm của \[BD\] hay \[IB = ID.\]
Khi đó \[MI\] là đường trung bình của \(\Delta BDE\) nên \(MI = \frac{1}{2}ED.\)
Tương tự, trong DCDE ta cũng có \(KN = \frac{1}{2}ED,\) trong DBCE có \(MK = \frac{1}{2}BC.\)
Ta có \(IK = MK - MI = \frac{1}{2}BC - \frac{1}{2}ED = ED - \frac{1}{2}ED = \frac{1}{2}ED\).
Do đó \(MI = IK = KN = \frac{1}{2}ED\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(13,97\% .\)
B. \(15,05\% .\)
C. \(15,04\% .\)
D. \(15,06\% .\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
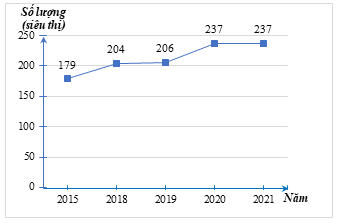
Năm 2020 số lượng siêu thị tăng \(\frac{{237 - 206}}{{206}} \cdot 100\% \approx 15,05\% \) so với năm 2019.
Câu 2
A. \(\frac{2}{5}.\)
B. \(\frac{5}{8}.\)
C. \(\frac{3}{4}.\)
D. \(\frac{3}{7}.\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Xác suất thực nghiệm của biến cố "Quả bóng lấy ra là quả bóng xanh dương" là:
\(\frac{{30 - 10 - 8}}{{30}} = \frac{{12}}{{30}} = \frac{2}{5}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(5,5{\rm{\;cm}}.\)
B. \(6,5{\rm{\;cm}}.\)
C. \(7{\rm{\;cm}}.\)
D. \(8{\rm{\;cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Chiều cao của các bạn học sinh nữ lớp 8A là số liệu rời rạc.
B. Số môn thể thao mà các bạn tổ 1 của lớp 8B biết chơi là số liệu liên tục.
C. Kết quả bơi 50 m tự do của 10 vận động viên là số liệu liên tục.
D. Nhiệt độ các ngày trong tuần ở Hà Nội là số liệu rời rạc.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{{AB}}{{AM}} = \frac{{BC}}{{MC}}.\)
B. \(\frac{{AB}}{{BC}} = \frac{{AM}}{{CM}}.\)
C. \[\frac{{BC}}{{AB}} = \frac{{AC}}{{AM}}.\]
D. \(AM = \frac{{AB \cdot AC}}{{AB + BC}} \cdot \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập