Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số \[1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4;{\rm{ }}5;{\rm{ }}6;{\rm{ }}7;{\rm{ }}8.\] Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần. Xác suất của biến cố: “Mũi tên chỉ vào hình quạt ghi số là ước của 12” là
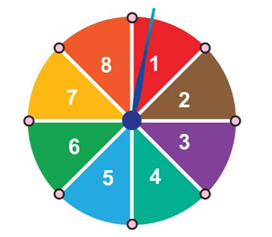
Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số \[1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4;{\rm{ }}5;{\rm{ }}6;{\rm{ }}7;{\rm{ }}8.\] Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần. Xác suất của biến cố: “Mũi tên chỉ vào hình quạt ghi số là ước của 12” là

Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: B
Trong 8 số \[1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4;{\rm{ }}5;{\rm{ }}6;{\rm{ }}7;{\rm{ }}8,\] có 5 số là ước của \(12\) là: \[1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4;{\rm{ }}6.\]
Xác suất của biến cố: “Mũi tên chỉ vào hình quạt ghi số là ước của 12” là: \(\frac{5}{8}.\)Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
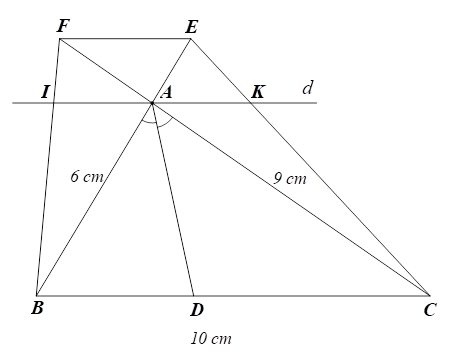
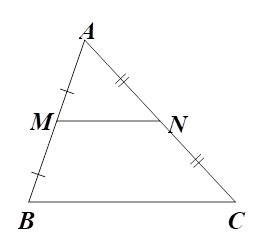
a) Xét \(\Delta ABC\) có \(AD\) là tia phân giác của \(\widehat {BAC},\) nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\) (tính chất đường phân giác), suy ra \(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}.\)
Theo tính chất dãy tỉ số bằng nhau ta có
\(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}} = \frac{{AB + AC}}{{DB + DC}} = \frac{{AB + AC}}{{BC}} = \frac{{6 + 9}}{{10}} = \frac{{15}}{{10}} = \frac{3}{2}.\)
Suy ra \(DB = \frac{2}{3}AB = \frac{2}{3} \cdot 6 = 4{\rm{\;cm}},\,\,DC = \frac{2}{3}AC = \frac{2}{3} \cdot 9 = 6{\rm{\;cm}}.\)
b) Từ \(AE = \frac{1}{3}AB\) suy ra \(\frac{{AE}}{{AB}} = \frac{1}{3}.\)
Từ \(AC = 3AF\) suy ra \(\frac{{AF}}{{AC}} = \frac{1}{3}.\)
Do đó \(\frac{{AE}}{{AB}} = \frac{{AF}}{{AC}} = \frac{1}{3}.\)
Theo định lí Thalès đảo ta có \(EF\,{\rm{//}}\,BC.\)
c) i) Xét \(\Delta FBC\) có \(IA\,{\rm{//}}\,BC\) (do \(d\,{\rm{//}}\,BC)\) nên theo hệ quả định lí Thalès ta có: \(\frac{{FI}}{{FB}} = \frac{{AF}}{{FC}} = \frac{{IA}}{{BC}}.\,\,\,\left( 1 \right)\)
Xét \(\Delta EBC\) có \(AK\,{\rm{//}}\,BC\) (do \(d\,{\rm{//}}\,BC)\) nên theo hệ quả định lí Thalès ta có: \(\frac{{EA}}{{EB}} = \frac{{AK}}{{BC}}.\,\,\,\left( 2 \right)\)
Xét \(\Delta ABC\) có \(EF\,{\rm{//}}\,BC\) (câu b) theo hệ quả định lí Thalès ta có: \(\frac{{AE}}{{AB}} = \frac{{AF}}{{AC}} = \frac{{EF}}{{BC}},\) suy ra \(\frac{{AE}}{{AE + AB}} = \frac{{AF}}{{AF + AC}},\) hay \(\frac{{AE}}{{EB}} = \frac{{AF}}{{FC}}.\,\,\,\left( 3 \right)\)
Từ (1), (2) và (3) suy ra \(\frac{{IA}}{{BC}} = \frac{{AK}}{{BC}},\) do đó \(AI = AK,\) hay \(A\) là trung điểm của \(IK.\)
ii) Xét \(\Delta EBC\) có \(AK\,{\rm{//}}\,BC\) (do \(d\,{\rm{//}}\,BC)\) nên theo hệ quả định lí Thalès ta có: \(\frac{{CK}}{{CE}} = \frac{{CA}}{{CF}}.\,\,\,\left( 4 \right)\)
Từ (1) và (4) ta có \(\frac{{FI}}{{FB}} + \frac{{CK}}{{CE}} = \frac{{AF}}{{FC}} + \frac{{CA}}{{CF}} = \frac{{FC}}{{FC}} = 1.\)
Vậy \(\frac{{FI}}{{FB}} + \frac{{CK}}{{CE}} = 1.\)
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
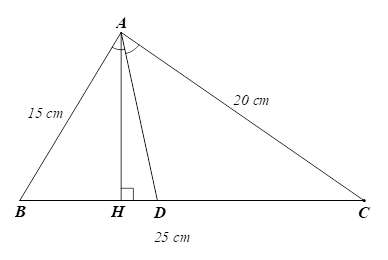
Xét \(\Delta ABC\) có \(AD\) là đường phân giác của \(\widehat {BAC}\) nên \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} = \frac{{15}}{{20}} = \frac{3}{4}.\)
Ta có: \({S_{\Delta ABD}} = \frac{1}{2}AH \cdot DB;\,\,{S_{\Delta ACD}} = \frac{1}{2}AH \cdot DC.\)
Do đó \[\frac{{{S_{\Delta ABD}}}}{{{S_{\Delta ACD}}}} = \frac{{\frac{1}{2}AH \cdot DB}}{{\frac{1}{2}AH \cdot DC}} = \frac{{DB}}{{DC}} = \frac{3}{4}.\]Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.