Cho \(\Delta ABC\) có \(\widehat A = 40^\circ ,\widehat B - \widehat C = 20^\circ \) trên tia đối của \(AC\) lấy điểm \(E\) sao cho \(AE = AB\). Hỏi số đo của \(\widehat {CBE}\) bằng bao nhiêu độ?

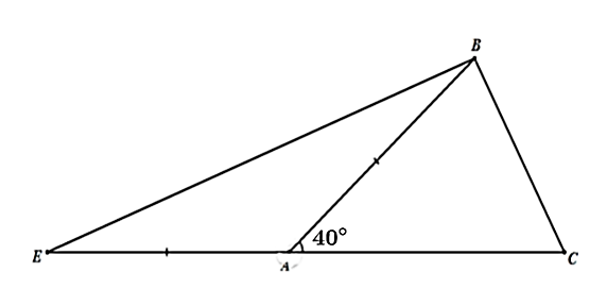
Xét \(\Delta ABC\) có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác) nên \(\widehat B + \widehat C = 140^\circ \).

Lại thấy \(\widehat B - \widehat C = 20^\circ \), do đó \(B = \frac{{140^\circ  + 20^\circ }}{2} = 80^\circ \) và \(\widehat C = 60^\circ \).

Xét \(\Delta AEB\) cân tại \(A\) (do \(AE = AB\)) nên \(\widehat {AEB} = \widehat {ABE}\) (tính chất của tam giác cân) (1)

Lại có \(\widehat {BAC}\) là góc ngoài tam giác \(AEB\) nên \(\widehat {BAC} = \widehat {AEB} + \widehat {ABE}\) (2)

Từ (1) và (2) suy ra \(\widehat {ABE} = \frac{{\widehat {BAC}}}{2} = 20^\circ \).

Do đó, \(\widehat {CBE} = \widehat {CBA} + \widehat {ABE} = 80^\circ  + 20 = 100^\circ \).