Bạch Đằng sóng dậy một trời đông,
Cọc ngầm dựng thẳng khóa muôn dòng.
Nam Hán thuyền tan theo triều xuống,
Toàn quân đại thắng giữ non sông.

Chiến thắng Bạch Đằng năm 938 là đỉnh cao nghệ thuật quân sự, khi Ngô Quyền đã đoán định chính xác nhịp lên, xuống của thủy triều để nhử thủy quân Nam Hán vào sâu bên trong, rồi phản công đúng thời khắc nước rút, qua đó đánh đuổi được giặc xâm lăng ra khỏi bờ cõi. Để mô hình hóa chiến thuật “canh con nước” ấy dưới lăng kính Giải tích, ta xét bài toán sau:
Xét một bãi cọc được đóng sâu xuống bùn theo phương thẳng đứng; chiều cao mỗi cọc (tính từ mặt bùn đến đầu cọc) là \(2,4{\rm{ m}}\).
Gọi \(h\left( t \right)\) (tính bằng mét) là độ sâu mực nước tại bãi cọc (tính từ mặt bùn đến mặt nước) ở thời điểm \(t\) giờ, trong đó \(t = 0\) ứng với thời điểm 09:00 trong ngày với \(0 \le t \le 4\). Thời gian này, mực nước rút nên \(h\left( t \right)\) giảm theo quy luật \(h'\left( t \right) = - 0,25t - 0,05\) (mét/giờ). Biết rằng vào lúc 09:00, mực nước tại bãi cọc cao hơn mặt bùn \(3,3{\rm{ m}}\) (tức là \(h\left( 0 \right) = 3,3\left( {\rm{m}} \right)\)).
Khi Ngô Quyền phát lệnh phản công, ông biết rằng thuyền địch sẽ quay đầu tháo chạy và mất 12 phút để tới bãi cọc. Ngô Quyền muốn đúng lúc thuyền địch tới bãi cọc thì đầu cọc còn chìm dưới mặt nước \(0,5{\rm{ m}}\).
Xét tính đúng sai các mệnh đề sau:
Bạch Đằng sóng dậy một trời đông,
Cọc ngầm dựng thẳng khóa muôn dòng.
Nam Hán thuyền tan theo triều xuống,
Toàn quân đại thắng giữ non sông.

Chiến thắng Bạch Đằng năm 938 là đỉnh cao nghệ thuật quân sự, khi Ngô Quyền đã đoán định chính xác nhịp lên, xuống của thủy triều để nhử thủy quân Nam Hán vào sâu bên trong, rồi phản công đúng thời khắc nước rút, qua đó đánh đuổi được giặc xâm lăng ra khỏi bờ cõi. Để mô hình hóa chiến thuật “canh con nước” ấy dưới lăng kính Giải tích, ta xét bài toán sau:
Xét một bãi cọc được đóng sâu xuống bùn theo phương thẳng đứng; chiều cao mỗi cọc (tính từ mặt bùn đến đầu cọc) là \(2,4{\rm{ m}}\).
Gọi \(h\left( t \right)\) (tính bằng mét) là độ sâu mực nước tại bãi cọc (tính từ mặt bùn đến mặt nước) ở thời điểm \(t\) giờ, trong đó \(t = 0\) ứng với thời điểm 09:00 trong ngày với \(0 \le t \le 4\). Thời gian này, mực nước rút nên \(h\left( t \right)\) giảm theo quy luật \(h'\left( t \right) = - 0,25t - 0,05\) (mét/giờ). Biết rằng vào lúc 09:00, mực nước tại bãi cọc cao hơn mặt bùn \(3,3{\rm{ m}}\) (tức là \(h\left( 0 \right) = 3,3\left( {\rm{m}} \right)\)).
Khi Ngô Quyền phát lệnh phản công, ông biết rằng thuyền địch sẽ quay đầu tháo chạy và mất 12 phút để tới bãi cọc. Ngô Quyền muốn đúng lúc thuyền địch tới bãi cọc thì đầu cọc còn chìm dưới mặt nước \(0,5{\rm{ m}}\).
Xét tính đúng sai các mệnh đề sau:Quảng cáo
Trả lời:
a) \(h\left( t \right) = 3,3 - 0,125{t^2} - 0,05t\) (m) trên \([0;4]\)
· Ta có tốc độ thay đổi mực nước là \(h'\left( t \right) = - 0,25t - 0,05\). Hàm độ sâu mực nước \(h\left( t \right)\) là nguyên hàm của \(h'\left( t \right)\): \(h\left( t \right) = \int {\left( { - 0,25t - 0,05} \right)} dt = - 0,125{t^2} - 0,05t + C\)
· Điều kiện biên: Tại thời điểm \(t = 0\) (09:00), \(h\left( 0 \right) = 3,3\).
Thay vào ta được: \(3,3 = - 0,125{\left( 0 \right)^2} - 0,05\left( 0 \right) + C \Rightarrow C = 3,3\)
· Kết luận: \(h\left( t \right) = 3,3 - 0,125{t^2} - 0,05t\).
b) Từ 09:00 đến 10:00, mực nước giảm đúng \(0,19\) (m)
· Thời điểm: 09:00 ứng với \(t = 0\), 10:00 ứng với \(t = 1\).
· Độ giảm mực nước: \(\Delta h = h\left( 0 \right) - h\left( 1 \right)\).
o \(h\left( 0 \right) = 3,3\)
o \(h\left( 1 \right) = 3,3 - 0,125{\left( 1 \right)^2} - 0,05\left( 1 \right) = 3,3 - 0,175 = 3,125\)
o \(\Delta h = 3,3 - 3,125 = 0,175\) (m).
· Kết luận: Mực nước giảm \(0,175\) m, không phải \(0,19\) m.
c) Sau 149 phút kể từ thời điểm 09:00 thì đầu cọc vừa chạm mặt nước
· Điều kiện: Đầu cọc chạm mặt nước khi độ sâu mực nước bằng chiều cao cọc: \(h\left( t \right) = 2,4\).
\(3,3 - 0,125{t^2} - 0,05t = 2,4 \Leftrightarrow 0,125{t^2} + 0,05t - 0,9 = 0\)
· Giải phương trình: Tìm được nghiệm dương \(t \approx 2,49\) (giờ).
· Đổi sang phút: \(2,49 \times 60 \approx 149,4\) phút. Làm tròn đến hàng đơn vị là 149 phút.
d) Ngô Quyền phải phát lệnh phản công vào lúc 10:26
· Mục tiêu: Khi thuyền địch tới bãi cọc (sau khi phát lệnh 12 phút), đầu cọc chìm dưới mặt nước \(0,5\) m.
· Điều kiện tại thời điểm thuyền tới (\({t_2}\)): \(h\left( {{t_2}} \right) = {\rm{chieu cao coc}} + 0,5 = 2,4 + 0,5 = 2,9\) (m).
\(3,3 - 0,125t_2^2 - 0,05{t_2} = 2,9 \Leftrightarrow 0,125t_2^2 + 0,05{t_2} - 0,4 = 0\)
· Giải phương trình: Nghiệm dương \({t_2} \approx 1,6\) (giờ).
· Đổi sang phút: \(1,6 \times 60 = 96\) phút kể từ lúc 09:00. Vậy thuyền phải tới bãi cọc lúc: 09:00 + 96 phút = 10:36.
· Thời điểm phát lệnh (\({t_1}\)): Vì thuyền mất 12 phút để di chuyển tới bãi cọc, Ngô Quyền cần phát lệnh trước đó 12 phút: 10:36 - 12 phút = 10:24.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) Đúng
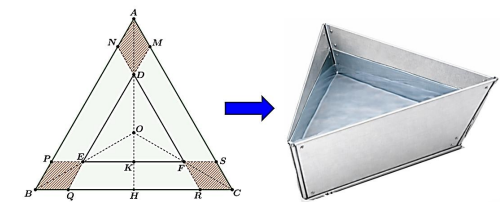
Ta có \(NP = QR = SM = AB - AN - BP = 6 - 2x\,(dm)\).
b) Đúng
Do tam giác \(ABC\) với cạnh bằng \(6\,dm\), nên \(AH = \sqrt {A{C^2} - C{H^2}} = 3\sqrt 3 \,(dm)\)
Và \(OA = \frac{2}{3}AH = 2\sqrt 3 \,(dm)\).
c) Đúng
Do \(AMDN\) là hình thoi cạnh \(x\) và \(\widehat {MAN} = {60^o}\),
Nên \(AD = \sqrt {A{N^2} + N{D^2} - 2AN.DN.cos{{120}^o}} = x\sqrt 3 \,(dm)\)
Lại có tam giác \(CMQ\) đều cạnh \(6 - x\,(dm)\)
Vậy \(DE = MQ - QE - DM = 6 - x - x - x = 6 - 3x\,(dm)\).
d) Đúng
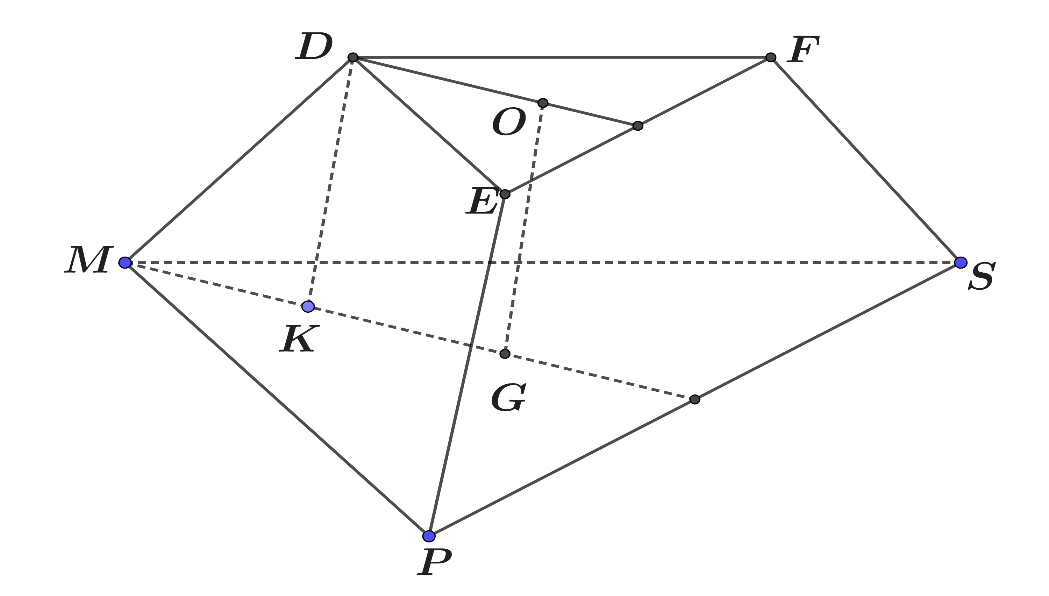
Ta có chóp cụt đều \(MPSDEF\) với cạnh đáy lớn \(MP = 6 - 2x\) và cạnh đáy nhỏ là \(DE = 6 - 3x\)
+) Ta có \({S_1} = {S_{DEF}} = \frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}\,(d{m^2})\).
+) Ta có \({S_2} = {S_{MPS}} = \frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4}\,(d{m^2})\).
+) Ta có \(\sqrt {{S_1}{S_2}} = \sqrt {\frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4} \times \frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}} = \frac{{(6 - 3x)(6 - 2x)\sqrt 3 }}{4}\,(d{m^2})\).
Kẻ \(DK \bot MG\,(K \in MG)\).
Ta tính \(h = OG = DK = \sqrt {M{D^2} - M{K^2}} \)
+) Ta có \(MD = x,\,\,MK = MG - KG = MG - DO = \frac{2}{3}\left( {6 - 2x} \right).\frac{{\sqrt 3 }}{2} - \frac{2}{3}\left( {6 - 3x} \right).\frac{{\sqrt 3 }}{2} = \frac{{x\sqrt 3 }}{3}\)\( \Rightarrow h = OG = \sqrt {{x^2} - {{\left( {\frac{{x\sqrt 3 }}{3}} \right)}^2}} = \frac{{x\sqrt 6 }}{3}\,(dm)\)
Thể tích chóp cụt đều bằng
\(\begin{array}{l}V = \frac{h}{3}\left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right)\\\,\,\,\,\, = \frac{{x\sqrt 6 }}{{3.3}}\left( {\frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}\, + \frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4} + \frac{{(6 - 3x)(6 - 2x)\sqrt 3 }}{4}} \right)\\\,\,\,\,\, = \frac{{\sqrt {18} }}{{36}}\left( {19{x^3} - 90{x^2} + 108x} \right)\end{array}\)
Dùng casio xét trên khoảng \(\left( {0;2} \right)\), ta có \(\mathop {max}\limits_{\left( {0;2} \right)} V \approx 4,54\,(d{m^3})\).
Lời giải
Đáp án: 7,02.
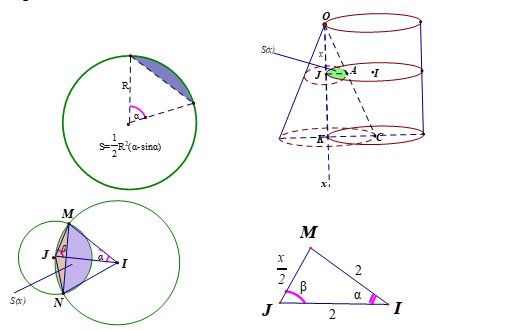
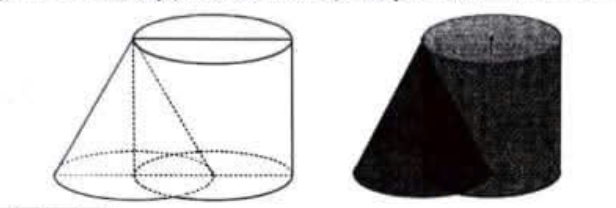
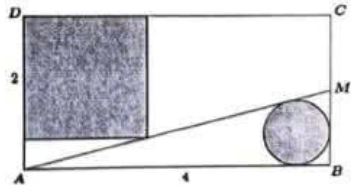
Gắn trục Ox như hình. Cắt khối giao của nón và trụ bởi 1 mặt phẳng vuông góc trục Ox tại x. Thiết diện là hình hợp bởi 2 hình viên phân của nón và trụ, có diện tích là S(x).
Xét tam giác OKC, có JA// KC, nên \[\frac{x}{4} = \frac{{JA}}{{KC}} = \frac{{JA}}{2} \Rightarrow JA = \frac{x}{2}\] là bán kính của đường tròn của hình nón tại vị trí x, tâm J. Đường tròn của hình trụ tại vị trí x có tâm I, bán kính bằng 2.
Gọi M là giao điểm của hai đường tròn tâm I và tâm J.
Giả sử \[\widehat {{\rm{MIJ}}} = \alpha \Rightarrow \widehat {{\rm{MIN}}} = 2\alpha ;\widehat {{\rm{MJI}}} = \beta \Rightarrow \widehat {{\rm{MJN}}} = 2\beta \].
Xét đường tròn tâm I, có \[IM = IN = JI = 2\]Xét đường tròn tâm J, có \[JM = JA = \frac{x}{2}\].
Áp đụng định lí cosin vào tam giác IJM, ta tính được:
\[cos\alpha = 1 - \frac{{{x^2}}}{{32}} \Rightarrow \alpha = {\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}});cos\beta = \frac{x}{8} \Rightarrow \beta = {\rm{ar}}cos\frac{x}{8}\]
Suy ra diện tích viên phân của đường tròn tâm I: \[{S_1} = 2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}))\]
Diện tích viên phân của đường tròn tâm J: \[{S_2} = \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8})\]
Nên diện tích thiết diện:
\[S(x) = {S_1} + {S_2} = 2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}})) + \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8})\]
Vậy thể tích phần giao của trụ và nón:
\[V = \int\limits_0^4 {S(x)dx = \int\limits_0^4 {(2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}})) + \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8}))dx} } = 7,02\]
(Theo Casio ta có kết quả trên)
Đáp số: 7,02.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.