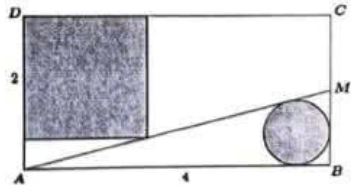
Bạn Xuân Anh có một tờ giấy cứng hình chữ nhật \(ABCD\) với \(AB = 4\,dm,\,\,AD = 2\,dm.\) Bạn chọn một điểm \(M\) thuộc cạnh \(BC\) rồi dùng thước kẻ vạch và cắt tờ giấy theo đường thẳng \(AM,\) chia tờ giấy thành hai phần.
Phần mảnh giấy chứa cạnh \(CD:\) Bạn muốn cắt được một hình vuông có đỉnh \(D,\) hai cạnh nằm trên đường \(DA\) và \(DC,\) đỉnh còn lại hình vuông thuộc đường cắt \(AM.\)
Phần mảnh giấy chứa cạnh \(AB:\) Bạn muốn cắt được một hình tròn sao cho hình tròn tiếp xúc với cả ba cạnh tam giác \(ABM.\)
Gọi \(S\)(phần tô đậm trong hình vẽ) là tổng diện tích của hình vuông và hình tròn cắt được. Hỏi khi \(M\) di động trên \(SB,\) giá trị nhỏ nhất của \(S\)bằng bao nhiêu \(dm\) (làm tròn đến hàng phần trăm)?
Bạn Xuân Anh có một tờ giấy cứng hình chữ nhật \(ABCD\) với \(AB = 4\,dm,\,\,AD = 2\,dm.\) Bạn chọn một điểm \(M\) thuộc cạnh \(BC\) rồi dùng thước kẻ vạch và cắt tờ giấy theo đường thẳng \(AM,\) chia tờ giấy thành hai phần.
Phần mảnh giấy chứa cạnh \(CD:\) Bạn muốn cắt được một hình vuông có đỉnh \(D,\) hai cạnh nằm trên đường \(DA\) và \(DC,\) đỉnh còn lại hình vuông thuộc đường cắt \(AM.\)
Phần mảnh giấy chứa cạnh \(AB:\) Bạn muốn cắt được một hình tròn sao cho hình tròn tiếp xúc với cả ba cạnh tam giác \(ABM.\)
Gọi \(S\)(phần tô đậm trong hình vẽ) là tổng diện tích của hình vuông và hình tròn cắt được. Hỏi khi \(M\) di động trên \(SB,\) giá trị nhỏ nhất của \(S\)bằng bao nhiêu \(dm\) (làm tròn đến hàng phần trăm)?

Quảng cáo
Trả lời:
Đáp án:
Đáp án: 3,16
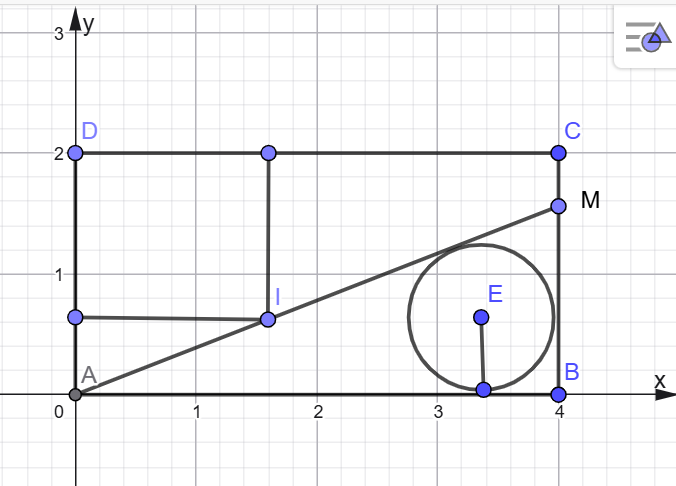
Chọn hệ tọa độ \(Oxy\) như hình vẽ ( đơn vị trên hệ trục là dm).
Ta có \(A(0;0),\,\,B(4;0),\,\,C(4;2),\,\,D(0;2).\)
Vì \(M\)thuộc cạnh \(BC\) nên \(M(4;m),\,\,(0 < m < 2).\)
Ta có \(AM = \sqrt {16 + {m^2}} \), Bán kính hình tròn nội tiếp tam giác \(ABM\) là
\(r = \frac{{{S_{ABM}}}}{p} = \frac{{\frac{1}{2}.AB.BM}}{{\frac{1}{2}(AB + BM + AM)}} = \frac{{4m}}{{4 + m + \sqrt {16 + {m^2}} }} = \frac{{4 + m - \sqrt {16 + {m^2}} }}{2}\) nên diện tích hình tròn là \({S_1} = \pi {r^2} = \pi {\left( {\frac{{4 + m - \sqrt {16 + {m^2}} }}{2}} \right)^2}\)
Gọi \(a,\,(0 < a < 2)\) là cạnh hìn vuông thì đỉnh đối diện với đỉnh \(D\) là đỉnh \(I(a;2 - a)\) thuộc đường
thẳng \(AM:\,y = \frac{m}{4}.x \Rightarrow 2 - a = \frac{m}{4}.a \Rightarrow a = \frac{8}{{4 + m}}\).
Suy ra diện tích hình vuông là \({S_2} = {a^2} = \frac{{64}}{{{{(4 + m)}^2}}}\)
Tổng diện tích hình vuông và hình tròn là
\(S(m) = {S_1} + {S_2} = \pi {\left( {\frac{{4 + m - \sqrt {16 + {m^2}} }}{2}} \right)^2} + \frac{{64}}{{{{(4 + m)}^2}}}\), với \(0 < m < 2.\)
Table ta được giá trị tổng diện tích nhỏ nhất xấp xỉ \(3,16\,(d{m^2})\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) Đúng
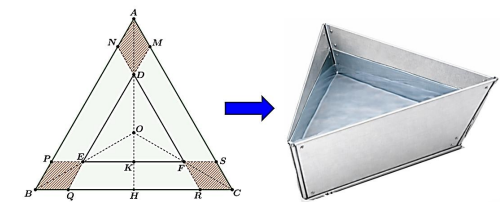
Ta có \(NP = QR = SM = AB - AN - BP = 6 - 2x\,(dm)\).
b) Đúng
Do tam giác \(ABC\) với cạnh bằng \(6\,dm\), nên \(AH = \sqrt {A{C^2} - C{H^2}} = 3\sqrt 3 \,(dm)\)
Và \(OA = \frac{2}{3}AH = 2\sqrt 3 \,(dm)\).
c) Đúng
Do \(AMDN\) là hình thoi cạnh \(x\) và \(\widehat {MAN} = {60^o}\),
Nên \(AD = \sqrt {A{N^2} + N{D^2} - 2AN.DN.cos{{120}^o}} = x\sqrt 3 \,(dm)\)
Lại có tam giác \(CMQ\) đều cạnh \(6 - x\,(dm)\)
Vậy \(DE = MQ - QE - DM = 6 - x - x - x = 6 - 3x\,(dm)\).
d) Đúng
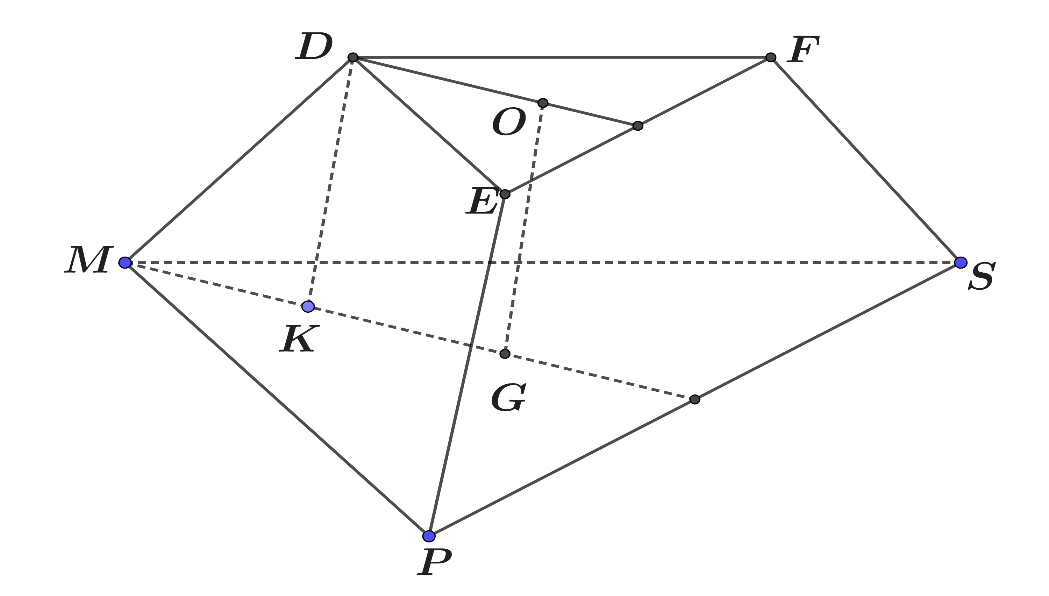
Ta có chóp cụt đều \(MPSDEF\) với cạnh đáy lớn \(MP = 6 - 2x\) và cạnh đáy nhỏ là \(DE = 6 - 3x\)
+) Ta có \({S_1} = {S_{DEF}} = \frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}\,(d{m^2})\).
+) Ta có \({S_2} = {S_{MPS}} = \frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4}\,(d{m^2})\).
+) Ta có \(\sqrt {{S_1}{S_2}} = \sqrt {\frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4} \times \frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}} = \frac{{(6 - 3x)(6 - 2x)\sqrt 3 }}{4}\,(d{m^2})\).
Kẻ \(DK \bot MG\,(K \in MG)\).
Ta tính \(h = OG = DK = \sqrt {M{D^2} - M{K^2}} \)
+) Ta có \(MD = x,\,\,MK = MG - KG = MG - DO = \frac{2}{3}\left( {6 - 2x} \right).\frac{{\sqrt 3 }}{2} - \frac{2}{3}\left( {6 - 3x} \right).\frac{{\sqrt 3 }}{2} = \frac{{x\sqrt 3 }}{3}\)\( \Rightarrow h = OG = \sqrt {{x^2} - {{\left( {\frac{{x\sqrt 3 }}{3}} \right)}^2}} = \frac{{x\sqrt 6 }}{3}\,(dm)\)
Thể tích chóp cụt đều bằng
\(\begin{array}{l}V = \frac{h}{3}\left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right)\\\,\,\,\,\, = \frac{{x\sqrt 6 }}{{3.3}}\left( {\frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}\, + \frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4} + \frac{{(6 - 3x)(6 - 2x)\sqrt 3 }}{4}} \right)\\\,\,\,\,\, = \frac{{\sqrt {18} }}{{36}}\left( {19{x^3} - 90{x^2} + 108x} \right)\end{array}\)
Dùng casio xét trên khoảng \(\left( {0;2} \right)\), ta có \(\mathop {max}\limits_{\left( {0;2} \right)} V \approx 4,54\,(d{m^3})\).
Lời giải
Đáp án: 7,02.
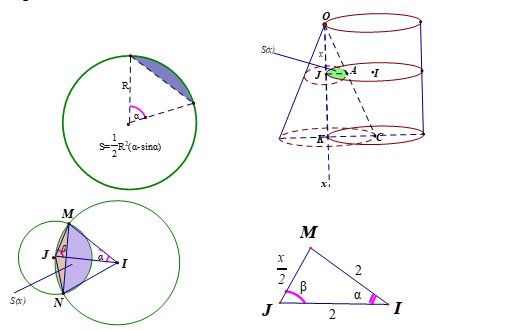
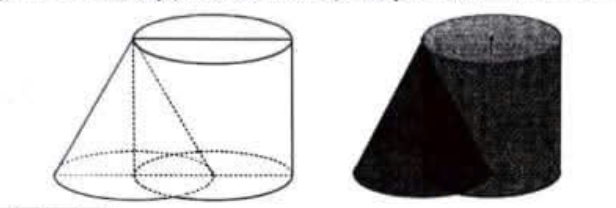
Gắn trục Ox như hình. Cắt khối giao của nón và trụ bởi 1 mặt phẳng vuông góc trục Ox tại x. Thiết diện là hình hợp bởi 2 hình viên phân của nón và trụ, có diện tích là S(x).
Xét tam giác OKC, có JA// KC, nên \[\frac{x}{4} = \frac{{JA}}{{KC}} = \frac{{JA}}{2} \Rightarrow JA = \frac{x}{2}\] là bán kính của đường tròn của hình nón tại vị trí x, tâm J. Đường tròn của hình trụ tại vị trí x có tâm I, bán kính bằng 2.
Gọi M là giao điểm của hai đường tròn tâm I và tâm J.
Giả sử \[\widehat {{\rm{MIJ}}} = \alpha \Rightarrow \widehat {{\rm{MIN}}} = 2\alpha ;\widehat {{\rm{MJI}}} = \beta \Rightarrow \widehat {{\rm{MJN}}} = 2\beta \].
Xét đường tròn tâm I, có \[IM = IN = JI = 2\]Xét đường tròn tâm J, có \[JM = JA = \frac{x}{2}\].
Áp đụng định lí cosin vào tam giác IJM, ta tính được:
\[cos\alpha = 1 - \frac{{{x^2}}}{{32}} \Rightarrow \alpha = {\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}});cos\beta = \frac{x}{8} \Rightarrow \beta = {\rm{ar}}cos\frac{x}{8}\]
Suy ra diện tích viên phân của đường tròn tâm I: \[{S_1} = 2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}))\]
Diện tích viên phân của đường tròn tâm J: \[{S_2} = \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8})\]
Nên diện tích thiết diện:
\[S(x) = {S_1} + {S_2} = 2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}})) + \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8})\]
Vậy thể tích phần giao của trụ và nón:
\[V = \int\limits_0^4 {S(x)dx = \int\limits_0^4 {(2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}})) + \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8}))dx} } = 7,02\]
(Theo Casio ta có kết quả trên)
Đáp số: 7,02.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.