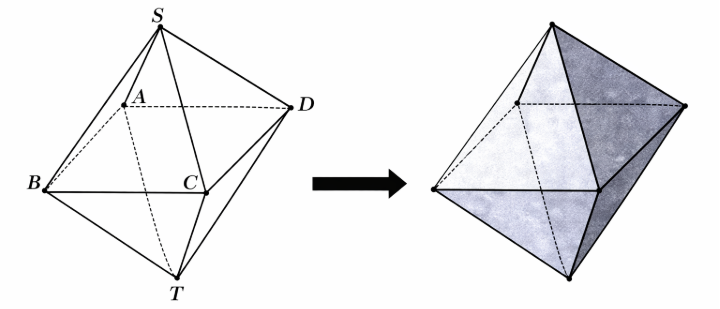
Một đèn lồng đón năm mới được thiết kế theo hình bát diện đều (ta có thể hình dung hình bát diện đều là hai hình chóp tứ giác đều có tất cả cạnh bằng nhau \(S.ABCD\) và \(T.ABCD\) sử dụng chung một mặt đáy). Nghệ nhân đã thiết kế sẵn 12 tấm bìa cứng là các tam giác bằng nhau gồm 3 màu xanh, đỏ, vàng; các tấm bìa cùng màu được đánh số từ 1 tới 4. Mỗi tấm bìa khi dán vào đèn lồng sẽ vừa kín một trong tám mặt bên của nó. Gọi \(N\) là số cách mà nghệ nhân có thể chọn 8 tấm bìa dán lên 8 mặt bên của đèn lồng sao cho hai tấm bìa có chung một cạnh thì khác màu, hai tấm bìa có chung đúng một đỉnh thì khác số. Giá trị \(\frac{N}{8} + 16\) bằng bao nhiêu?

Quảng cáo
Trả lời:
Đáp án:
Đáp án: 448.
Một hình bát diện đều có 8 mặt là các tam giác đều. Đây là 8 mặt bên của đèn lồng.
Các mặt của hình bát diện đều có thể được chia thành hai tập hợp \({C_1}\) và \({C_2}\), mỗi tập hợp gồm 4 mặt, sao cho bất kỳ hai mặt nào kề nhau (chung một cạnh) đều thuộc các tập hợp khác nhau. Ví dụ, nếu các đỉnh là \(S\) (trên), \(T\) (dưới) và \(A,B,C,D\) (mặt phẳng giữa), thì:
Tập hợp
Tập hợp
Bất kỳ hai mặt nào trong cùng một tập hợp \({C_1}\) hoặc \({C_2}\) đều không kề nhau (không chung cạnh).
Điều kiện 1: Hai tấm bìa có chung một cạnh thì khác màu.
Điều này có nghĩa là tất cả các mặt trong tập hợp \({C_1}\) phải có cùng một màu (ví dụ, màu X), và tất cả các mặt trong tập hợp \({C_2}\) phải có cùng một màu khác (ví dụ, màu Y), với \(X \ne Y\).
Số cách chọn 2 màu từ 3 màu có sẵn (xanh, đỏ, vàng) là \(\left( \begin{array}{c}3\\2\end{array} \right) = 3\) cách.
Sau khi chọn 2 màu (ví dụ: X và Y), có 2 cách để gán chúng cho hai tập hợp \({C_1}\) và \({C_2}\):
1. \({C_1}\) có màu X, \({C_2}\) có màu Y.
2. \({C_1}\) có màu Y, \({C_2}\) có màu X.
Vậy, tổng số cách để xác định màu cho 8 mặt là \(3 \times 2 = 6\) cách.
Với mỗi cách xác định màu, chúng ta sẽ cần 4 tấm bìa của màu này và 4 tấm bìa của màu kia. Do mỗi màu có đủ 4 tấm bìa được đánh số từ 1 đến 4, nên việc lựa chọn 8 tấm bìa cụ thể được xác định ngay khi chọn và gán màu. Ví dụ, nếu \({C_1}\) là màu xanh và \({C_2}\) là màu đỏ, chúng ta sẽ sử dụng tất cả 4 tấm bìa xanh (X1, X2, X3, X4) và tất cả 4 tấm bìa đỏ (Đ1, Đ2, Đ3, Đ4).
Điều kiện 2: Hai tấm bìa có chung đúng một đỉnh thì khác số.
Trước hết, cần xác định các cặp mặt chung đúng một đỉnh.
Nếu hai mặt kề nhau (chung một cạnh), chúng chung hai đỉnh, không phải chung đúng một đỉnh.
Nếu hai mặt thuộc hai tập hợp màu khác nhau (\({C_1}\) và \({C_2}\)), chúng sẽ kề nhau (chung một cạnh).
Ví dụ: và chung cạnh \(SB\).
Ví dụ: và không chung đỉnh nào.
Do đó, điều kiện này chỉ áp dụng cho các cặp mặt có cùng màu (nghĩa là chúng thuộc cùng một tập hợp \({C_1}\) hoặc \({C_2}\)).
Hãy liệt kê các cặp mặt chung đúng một đỉnh trong tập hợp \({C_1}\):
1. và chung đỉnh \(S\).
2. và chung đỉnh \(T\).
3. và chung đỉnh \(A\).
4. và chung đỉnh \(B\).
5. và chung đỉnh \(C\).
6. và chung đỉnh \(D\).
Điều kiện "khác số" cho các cặp này có nghĩa là 4 tấm bìa của màu X được đặt trên 4 mặt của \({C_1}\) phải có các số khác nhau. Vì chúng ta có sẵn 4 tấm bìa của mỗi màu được đánh số 1, 2, 3, 4, nên việc sử dụng 4 tấm bìa này để dán lên 4 mặt đảm bảo rằng các số đều khác nhau.
Số cách sắp xếp 4 tấm bìa (ví dụ: X1, X2, X3, X4) lên 4 mặt của tập hợp \({C_1}\) là \(4!\) cách.
Tương tự, với tập hợp \({C_2}\):
1. và chung đỉnh \(S\).
2. và chung đỉnh \(T\).
3. và chung đỉnh \(C\).
4. và chung đỉnh \(B\).
5. và chung đỉnh \(A\).
6. và chung đỉnh \(D\).
Điều kiện này có nghĩa là 4 tấm bìa của màu Y được đặt trên 4 mặt của \({C_2}\) phải có các số khác nhau. Vì chúng ta có sẵn 4 tấm bìa của mỗi màu được đánh số 1, 2, 3, 4, nên việc sử dụng 4 tấm bìa này để dán lên 4 mặt đảm bảo rằng các số đều khác nhau.
Số cách sắp xếp 4 tấm bìa (ví dụ: Đ1, Đ2, Đ3, Đ4) lên 4 mặt của tập hợp \({C_2}\) là \(4!\) cách.
Tính \(N\):
\(\begin{array}{l}N = ({\rm{So c\'a ch chon v\`a g\'a n m\`a u}}) \times ({\rm{So c\'a ch sap xep 4 tam b\`i a cho }}{C_1})\\ \times ({\rm{So c\'a ch sap xep 4 tam b\`i a cho }}{C_2})\end{array}\)
\( \Rightarrow N = 6 \times 4! \times 4! = 3456\).
Suy ra: \(\frac{N}{8} + 16 = \frac{{3456}}{8} + 16 = 432 + 16 = 448\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) Đúng
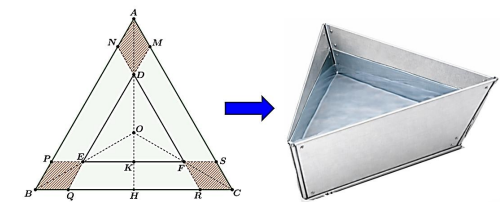
Ta có \(NP = QR = SM = AB - AN - BP = 6 - 2x\,(dm)\).
b) Đúng
Do tam giác \(ABC\) với cạnh bằng \(6\,dm\), nên \(AH = \sqrt {A{C^2} - C{H^2}} = 3\sqrt 3 \,(dm)\)
Và \(OA = \frac{2}{3}AH = 2\sqrt 3 \,(dm)\).
c) Đúng
Do \(AMDN\) là hình thoi cạnh \(x\) và \(\widehat {MAN} = {60^o}\),
Nên \(AD = \sqrt {A{N^2} + N{D^2} - 2AN.DN.cos{{120}^o}} = x\sqrt 3 \,(dm)\)
Lại có tam giác \(CMQ\) đều cạnh \(6 - x\,(dm)\)
Vậy \(DE = MQ - QE - DM = 6 - x - x - x = 6 - 3x\,(dm)\).
d) Đúng
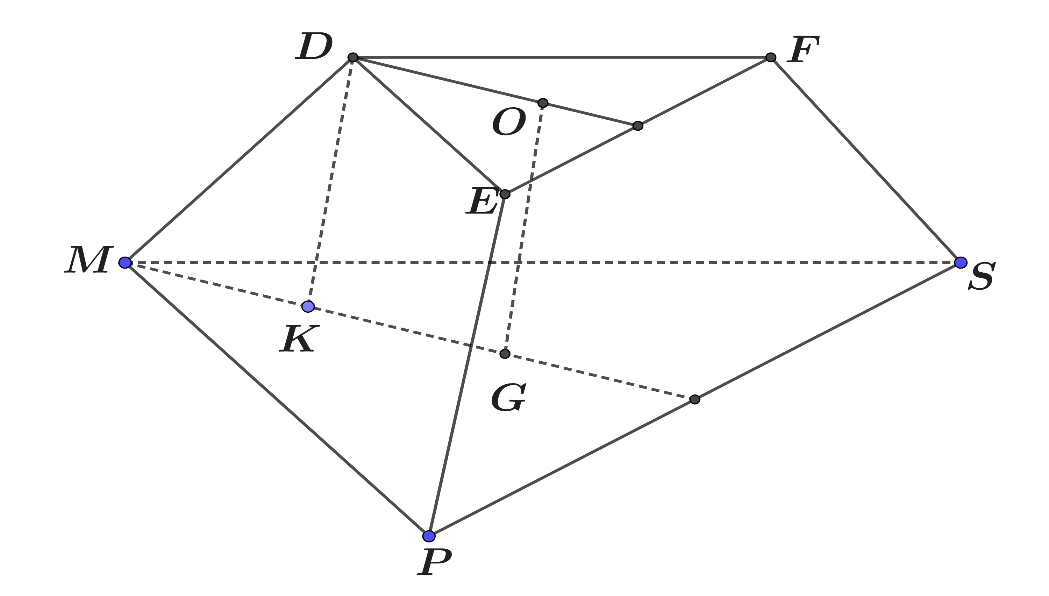
Ta có chóp cụt đều \(MPSDEF\) với cạnh đáy lớn \(MP = 6 - 2x\) và cạnh đáy nhỏ là \(DE = 6 - 3x\)
+) Ta có \({S_1} = {S_{DEF}} = \frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}\,(d{m^2})\).
+) Ta có \({S_2} = {S_{MPS}} = \frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4}\,(d{m^2})\).
+) Ta có \(\sqrt {{S_1}{S_2}} = \sqrt {\frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4} \times \frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}} = \frac{{(6 - 3x)(6 - 2x)\sqrt 3 }}{4}\,(d{m^2})\).
Kẻ \(DK \bot MG\,(K \in MG)\).
Ta tính \(h = OG = DK = \sqrt {M{D^2} - M{K^2}} \)
+) Ta có \(MD = x,\,\,MK = MG - KG = MG - DO = \frac{2}{3}\left( {6 - 2x} \right).\frac{{\sqrt 3 }}{2} - \frac{2}{3}\left( {6 - 3x} \right).\frac{{\sqrt 3 }}{2} = \frac{{x\sqrt 3 }}{3}\)\( \Rightarrow h = OG = \sqrt {{x^2} - {{\left( {\frac{{x\sqrt 3 }}{3}} \right)}^2}} = \frac{{x\sqrt 6 }}{3}\,(dm)\)
Thể tích chóp cụt đều bằng
\(\begin{array}{l}V = \frac{h}{3}\left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right)\\\,\,\,\,\, = \frac{{x\sqrt 6 }}{{3.3}}\left( {\frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}\, + \frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4} + \frac{{(6 - 3x)(6 - 2x)\sqrt 3 }}{4}} \right)\\\,\,\,\,\, = \frac{{\sqrt {18} }}{{36}}\left( {19{x^3} - 90{x^2} + 108x} \right)\end{array}\)
Dùng casio xét trên khoảng \(\left( {0;2} \right)\), ta có \(\mathop {max}\limits_{\left( {0;2} \right)} V \approx 4,54\,(d{m^3})\).
Lời giải
Đáp án: 7,02.
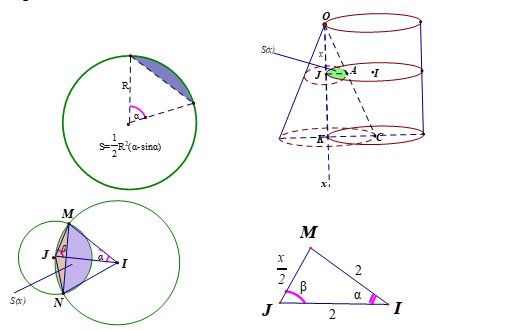
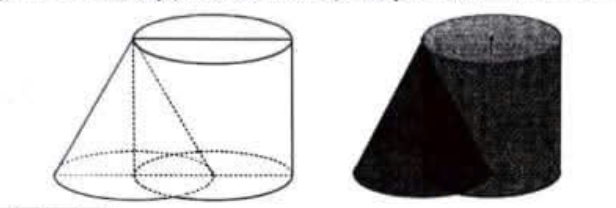
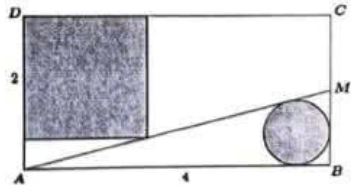
Gắn trục Ox như hình. Cắt khối giao của nón và trụ bởi 1 mặt phẳng vuông góc trục Ox tại x. Thiết diện là hình hợp bởi 2 hình viên phân của nón và trụ, có diện tích là S(x).
Xét tam giác OKC, có JA// KC, nên \[\frac{x}{4} = \frac{{JA}}{{KC}} = \frac{{JA}}{2} \Rightarrow JA = \frac{x}{2}\] là bán kính của đường tròn của hình nón tại vị trí x, tâm J. Đường tròn của hình trụ tại vị trí x có tâm I, bán kính bằng 2.
Gọi M là giao điểm của hai đường tròn tâm I và tâm J.
Giả sử \[\widehat {{\rm{MIJ}}} = \alpha \Rightarrow \widehat {{\rm{MIN}}} = 2\alpha ;\widehat {{\rm{MJI}}} = \beta \Rightarrow \widehat {{\rm{MJN}}} = 2\beta \].
Xét đường tròn tâm I, có \[IM = IN = JI = 2\]Xét đường tròn tâm J, có \[JM = JA = \frac{x}{2}\].
Áp đụng định lí cosin vào tam giác IJM, ta tính được:
\[cos\alpha = 1 - \frac{{{x^2}}}{{32}} \Rightarrow \alpha = {\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}});cos\beta = \frac{x}{8} \Rightarrow \beta = {\rm{ar}}cos\frac{x}{8}\]
Suy ra diện tích viên phân của đường tròn tâm I: \[{S_1} = 2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}))\]
Diện tích viên phân của đường tròn tâm J: \[{S_2} = \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8})\]
Nên diện tích thiết diện:
\[S(x) = {S_1} + {S_2} = 2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}})) + \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8})\]
Vậy thể tích phần giao của trụ và nón:
\[V = \int\limits_0^4 {S(x)dx = \int\limits_0^4 {(2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}})) + \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8}))dx} } = 7,02\]
(Theo Casio ta có kết quả trên)
Đáp số: 7,02.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.