Một hộp đựng \(6\) bi xanh đánh số từ \(1\) đến \(6\), \(7\) bi vàng đánh số từ \(1\) đến \(7\) và \(8\) bi đỏ đánh số từ \(1\) đến \(8\). Lấy ngẫu nhiên \(3\) bi từ hộp. Xác suất để ba bi lấy được có \(3\) số khác nhau và khác màu là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Số phần tử không gian mẫu là: \(\left| \Omega \right| = C_{21}^3\).
Gọi \(A\) là biến cố ba bi lấy được có 3 số khác nhau và 3 màu khác nhau.
Cách 1.
Ta có các trường hợp sau:
Trường hợp 1. Bi đỏ được chọn ghi số \(8\). Khi đó có hai khả năng sau:
Khả năng 1. Bi vàng được chọn ghi số \(7\). Khi đó có \(6\) cách chọn bi xanh.
Khả năng 2. Bi vàng được chọn ghi số bé hơn \(7\). Khi đó bi vàng có \(6\) cách chọn, bi xanh có \(5\) cách chọn.
Trường hợp 1 có \(6 + 6 \cdot 5 = 36\) cách chọn.
Trường hợp 2. Bi đỏ được chọn ghi số \(7\). Khi đó bi vàng có \(6\) cách chọn (từ \(1\) đến \(6\)) và bi xanh có \(5\) cách chọn (vì ghi số phải khác số bi vàng). Trường hợp này có \(6 \cdot 5 = 30\) cách chọn.
Trường hợp 3. Bi đỏ được chọn ghi số bé hơn \(7\). Bi đỏ có \(6\) cách chọn.
Khả năng 1. Bi vàng được chọn ghi số \(7\). Khi đó bi xanh có \(5\) cách chọn (ghi số khác bi đỏ).
Khả năng 2. Bi vàng được chọn ghi số bé hơn \(7\) và khác số bi đỏ. Khi đó bi vàng có \(5\) cách chọn và bi xanh có \(4\) cách chọn.
Trường hợp 3 này có \(6\left( {5 + 5 \cdot 4} \right) = 150\) cách chọn.
Vậy số phần tử của biến cố \(A\) là: \(\left| A \right| = 36 + 30 + 150 = 216\).
Vậy xác suất cần tìm là: \(P\left( A \right) = \frac{{216}}{{C_{21}^3}} = \frac{{108}}{{665}}\).
Cách 2.
Có \(6\) cách chọn bi xanh.
Với mỗi cách chọn bi xanh có \(6\) cách chọn bi vàng để bi vàng ghi số khác với bi xanh.
Với mỗi cách chọn bi xanh và bi vàng có \(6\) cách chọn bi đỏ ghi số khác với bi vàng, bi xanh.
Vậy số phần tử của biến cố \(A\) là: \(\left| A \right| = {6^3}\).
Xác suất cần tìm là: \(P\left( A \right) = \frac{{{6^3}}}{{C_{21}^3}} = \frac{{108}}{{665}}\). Chọn B.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi biến cố A: “Học sinh đó chọn tổ hợp A00” ;
biến cố B: “Học sinh đó đỗ đại học”.
Ta cần tính \[P\left( {A|B} \right)\].
Theo bài ra ta có: \(P\left( A \right) = 0,8;P\left( {\overline A } \right) = 1 - P\left( A \right) = 1 - 0,8 = 0,2\).
Ta có \(P\left( {B|A} \right)\) là xác suất để một học sinh đỗ đại học với điều kiện học sinh đó chọn tổ hợp A00 nên \(P\left( {B|A} \right) = 0,6\) và \(P\left( {B|\overline A } \right)\) là xác suất để một học sinh đỗ đại học với điều kiện học sinh đó không chọn tổ hợp A00 nên \(P\left( {B|\overline A } \right) = 0,7\).
Áp dụng công thức Bayes ta được
\(P\left( {A|B} \right) = \frac{{P\left( A \right) \cdot P\left( {B|A} \right)}}{{P\left( A \right) \cdot P\left( {B|A} \right) + P\left( {\overline A } \right) \cdot P\left( {B|\overline A } \right)}} = \frac{{0,8 \cdot 0,6}}{{0,8 \cdot 0,6 + 0,2 \cdot 0,7}} = \frac{{24}}{{31}}\).
Trả lời: \(\frac{{24}}{{31}}\).
Câu 2
Lời giải
Ta có \(f'\left( x \right) = \left( {x - 2} \right)\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 1\end{array} \right..\)
Bảng xét dấu của \(f'\left( x \right)\) như sau:
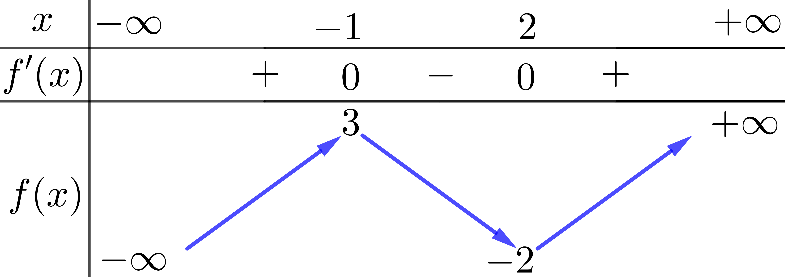
Vậy hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right),\left( {2; + \infty } \right)\) và nghịch biến trên khoảng \[\left( { - 1;2} \right)\].
Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập