Phần III (1 điểm). Thí sinh trả lời từ câu 1 đến câu 4. Đối với mỗi câu, thí sinh chỉ viết kết quả, không trình bày suy luận. Đối với mỗi câu trả lời đúng, thí sinh được 0,25 điểm.
Giám đốc một nhà hát đang phân vân trong việc xác định mức giá vé xem các chương trình được trình chiếu trong nhà hát. Việc này rất quan trọng nó sẽ quyết định nhà hát thu được bao nhiêu lợi nhuận từ các buổi trình chiếu. Theo những cuốn sổ ghi chép của mình, ông ta xác định được rằng: nếu giá vé vào cửa là \[200\] nghìn đồng/người thì trung bình có \[1000\] người đến xem. Nhưng nếu tăng thêm 10 nghìn đồng /người thì sẽ mất \[100\] khách hàng hoặc giảm đi \[10\] nghìn đồng /người thì sẽ có thêm \[100\] khách hàng trong số trung bình.Biết rằng, trung bình, mỗi khách hàng còn đem lại \[20\] nghìn đồng lợi nhuận cho nhà hát trong các dịch vụ đi kèm. Hãy giúp giám đốc nhà hát này xác định xem cần tính giá vé vào cửa là bao nhiêu nghìn đồng để thu nhập là lớn nhất?
Phần III (1 điểm). Thí sinh trả lời từ câu 1 đến câu 4. Đối với mỗi câu, thí sinh chỉ viết kết quả, không trình bày suy luận. Đối với mỗi câu trả lời đúng, thí sinh được 0,25 điểm.
Giám đốc một nhà hát đang phân vân trong việc xác định mức giá vé xem các chương trình được trình chiếu trong nhà hát. Việc này rất quan trọng nó sẽ quyết định nhà hát thu được bao nhiêu lợi nhuận từ các buổi trình chiếu. Theo những cuốn sổ ghi chép của mình, ông ta xác định được rằng: nếu giá vé vào cửa là \[200\] nghìn đồng/người thì trung bình có \[1000\] người đến xem. Nhưng nếu tăng thêm 10 nghìn đồng /người thì sẽ mất \[100\] khách hàng hoặc giảm đi \[10\] nghìn đồng /người thì sẽ có thêm \[100\] khách hàng trong số trung bình.Biết rằng, trung bình, mỗi khách hàng còn đem lại \[20\] nghìn đồng lợi nhuận cho nhà hát trong các dịch vụ đi kèm. Hãy giúp giám đốc nhà hát này xác định xem cần tính giá vé vào cửa là bao nhiêu nghìn đồng để thu nhập là lớn nhất?
Câu hỏi trong đề: Đề ôn thi ĐGNL ĐHSP Hà Nội môn Toán có đáp án !!
Quảng cáo
Trả lời:
Đáp án:
Gọi \[x\] là số lần giá vé tăng/giảm 10 nghìn đồng.
Giá vé sau khi điều chỉnh là \[200 + \;10x{\rm{ }}\](nghìn đồng) \[\left( {200 + 10x > 0} \right)\].
Số khách là: \(1000 - 100x{\rm{ }}\left( {1000 - 100x > 0} \right)\).
Điều kiện: \[ - 20 < x < 10\].
Tổng thu nhập là: \[f\left( x \right) = \;\left( {200 + \;10x + \;20} \right)\left( {1000 - 100x} \right) = \; - 1000{x^2}\; - 1\;2000x + \;220\;000\].
Bảng biến thiên:
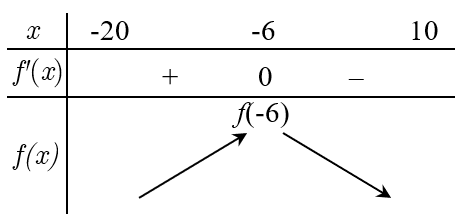
Vậy để thu nhập cao nhất thì \[x = - 6\], khi đó giá vé là \[200 + 10 \cdot \left( { - 6} \right) = 140\] (nghìn đồng).
Trả lời: 140.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
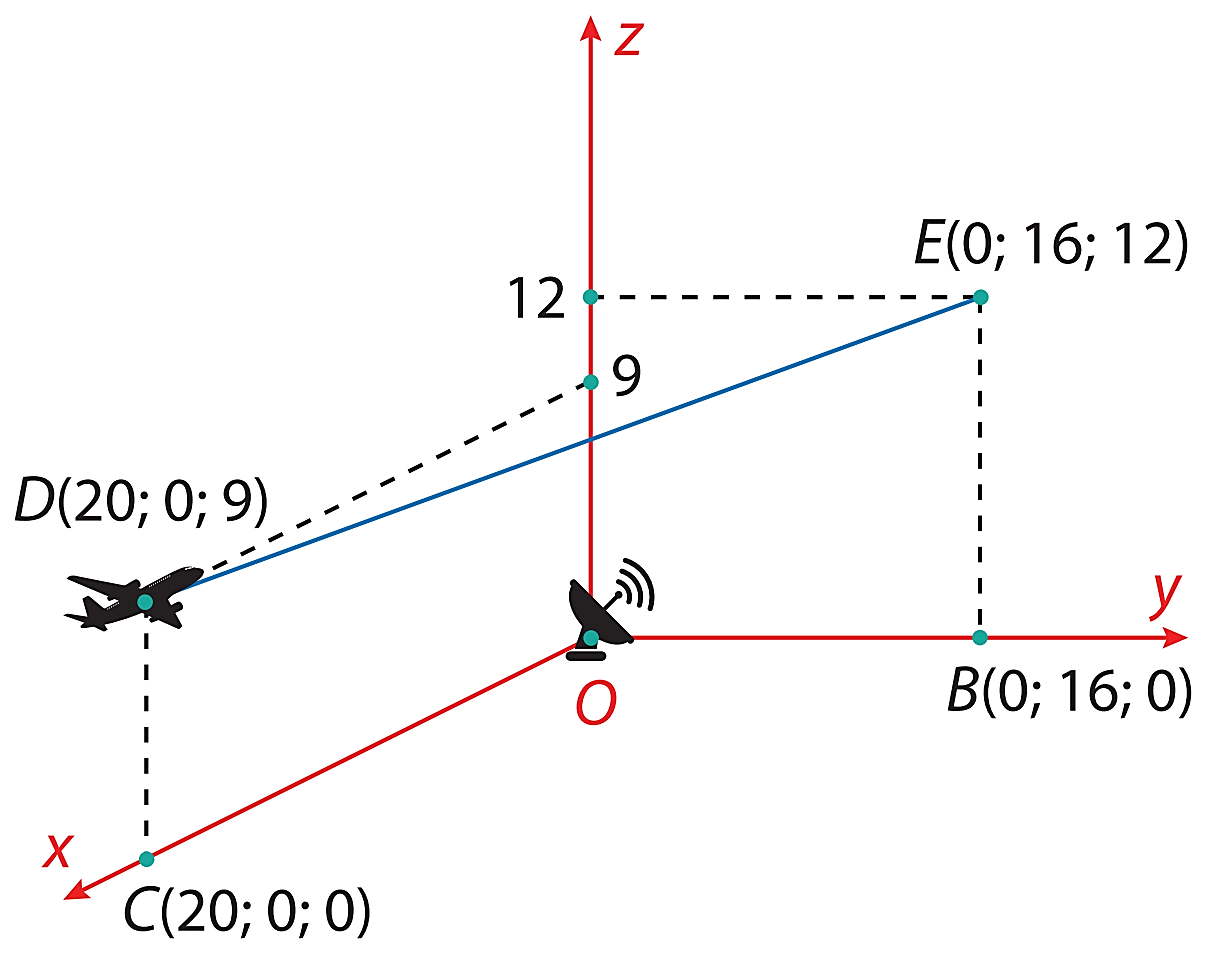
a) Sai. Ta có \(\overrightarrow {OD} = \left( {20\,;0\,;9} \right)\) và \(OD = \sqrt {{{20}^2} + {9^2}} = \sqrt {481} \)km \( \approx 22000\) m.
b) Đúng. Tọa độ trung điểm \(I\) của \(DE\) là \(\left( {10;8;\frac{{21}}{2}} \right).\)
Khi máy bay bay đến điểm \(I,\) máy bay cách mặt đất \(\frac{{21}}{2}\)km hay \(10500\)m.
c) Đúng. Ta có \(\overrightarrow {DE} = \left( { - 20;16;3} \right)\).
Đường thẳng \(DE\) đi qua điểm \(D\left( {20;0;9} \right)\) và có vectơ chỉ phương \(\vec u = \overrightarrow {DE} = \left( { - 20\,;16\,;3} \right)\) nên có phương trình tham số là \(\left\{ \begin{array}{l}x = 20 - 20t\\y = 16t\\z = 9 + 3t\end{array} \right.,(t \in \mathbb{R}).\)
Thay tọa độ điểm \(P\left( {16;3,2;9,6} \right)\) vào phương trình tham số của đường thẳng \(DE\) ta được
\(\left\{ \begin{array}{l}16 = 20 - 20t\\3,2 = 16t\\9,6 = 9 + 3t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 0,2\\t = 0,2\\t = 0,2\end{array} \right.\). Như vậy \(P \in DE.\)
Do đó trên đoạn đường bay từ \(D\) đến \(E,\) máy bay sẽ đi qua điểm \(P\left( {16;3,2;9,6} \right)\).
d) Sai. Gọi \(H\left( {20 - 20t;16t;9 + 3t} \right) \in DE\) là hình chiếu của \(O\) trên \(DE.\)
Hai vectơ \(\left\{ \begin{array}{l}\overrightarrow {OH} = \left( {20 - 20t;16t;9 + 3t} \right)\\\overrightarrow {DE} = \left( { - 20;16;3} \right)\end{array} \right.\) vuông góc với nhau nên
\(\overrightarrow {OH} \cdot \overrightarrow {DE} = 0 \Leftrightarrow - 20\left( {20 - 20t} \right) + 16 \cdot 16t + 3\left( {9 + 3t} \right) = 0 \Leftrightarrow t = \frac{{373}}{{665}}.\)
Khi đó \(\overrightarrow {OH} = \left( {\frac{{1168}}{{133}};\frac{{5968}}{{665}};\frac{{7104}}{{665}}} \right)\) và \(OH = \sqrt {{{\left( {\frac{{1168}}{{133}}} \right)}^2} + {{\left( {\frac{{5968}}{{665}}} \right)}^2} + {{\left( {\frac{{7104}}{{665}}} \right)}^2}} = \sqrt {\frac{{180736}}{{665}}} = \frac{{16\sqrt {469490} }}{{665}}.\)
Khoảng cách giữa vị trí đầu tiên và vị trí cuối cùng mà máy bay bay trong phạm vi theo dõi của ra đa là:
\(2\sqrt {{{20}^2} - O{H^2}} = 2\sqrt {{{20}^2} - \frac{{180736}}{{665}}} = \frac{{584\sqrt {665} }}{{665}} \approx 22600\) m.
Lời giải
Gọi \({A_k}\) là biến cố: “Người thợ săn bắn trúng thỏ ở lần thứ \(k\)”; \(k = 1,2,3.\)
Theo đầu bài ta có: \(P\left( {{A_1}} \right) = 0,5\); \(P\left( {{A_2}|\overline {{A_1}} } \right) = \frac{{20 \times 0,5}}{{30}} = \frac{1}{3}\); \(P\left( {{A_3}|\overline {{A_1}} \,\overline {{A_2}} } \right) = \frac{{20 \times 0,5}}{{50}} = \frac{1}{5}.\)
Gọi \(A\) là biến cố: “Người thợ săn bắn trúng thỏ”. Khi đó: \(A = {A_1} \cup \overline {{A_1}} {A_2} \cup \overline {{A_1}} \,\overline {{A_2}} {A_3}.\)
Vì \(3\) biến cố \({A_1}\), \(\overline {{A_1}} {A_2}\), \(\overline {{A_1}} \,\overline {{A_2}} {A_3}\) xung khắc từng đôi nên: \(P\left( A \right) = P\left( {{A_1}} \right) + P\left( {\overline {{A_1}} {A_2}} \right) + P\left( {\overline {{A_1}} \overline {{A_2}} {A_3}} \right).\)
Theo công thức nhân xác suất \(P\left( {\overline {{A_1}} {A_2}} \right) = P\left( {\overline {{A_1}} } \right) \cdot P\left( {{A_2}|\overline {{A_1}} } \right) = \left[ {1 - P\left( {{A_1}} \right)} \right] \cdot P\left( {{A_2}|\overline {{A_1}} } \right)\)\( = \left( {1 - 0,5} \right) \times \frac{1}{3} = \frac{1}{6}.\)
Tương tự \(P\left( {\overline {{A_1}} \,\overline {{A_2}} {A_3}} \right) = P\left( {\overline {{A_1}} } \right) \cdot P\left( {\overline {{A_2}} |\overline {{A_1}} } \right) \cdot P\left( {{A_3}|\overline {{A_1}} \,\overline {{A_2}} } \right)\)
\( = \left[ {1 - P\left( {{A_1}} \right)} \right] \cdot P\left[ {1 - P\left( {{A_2}|\overline {{A_1}} } \right)} \right] \cdot P\left( {{A_3}|\overline {{A_1}} \,\overline {{A_2}} } \right) = \left( {1 - 0,5} \right)\left( {1 - \frac{1}{3}} \right) \times \frac{1}{5} = \frac{1}{{15}}.\)
Do đó: \(P\left( A \right) = 0,5 + \frac{1}{6} + \frac{1}{{15}} = \frac{{11}}{{15}}.\)
Trả lời: \(\frac{{11}}{{15}}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.