Cho parabol \((P):y = {x^2}\) và đường thẳng \((d):y = - x + 2\).
1. Tìm tọa độ giao điểm \(A,B\left( {{x_A} > {x_B}} \right)\) của \((d)\) và \((P)\).
2. Tính diện tích tam giác \(OAB\).
Cho parabol \((P):y = {x^2}\) và đường thẳng \((d):y = - x + 2\).
1. Tìm tọa độ giao điểm \(A,B\left( {{x_A} > {x_B}} \right)\) của \((d)\) và \((P)\).
2. Tính diện tích tam giác \(OAB\).
Câu hỏi trong đề: Các dạng bài tập Hàm số y = ax^2 (a ≠ 0) lớp 9 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1. Phương trình hoành độ giao điểm \((d)\) và \((P)\)
\({x^2} = - x + 2 \Leftrightarrow {x^2} + x - 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = - 2.}\end{array}} \right.\)
Với \(x = 1 \Rightarrow y = 1\).
Với \(x = - 2 \Rightarrow y = 4\).
Vậy \((d)\) cắt \((P)\) tại hai điểm phân biệt có tọa độ \(A(1;1)\) và \(B( - 2;4)\).
2. Tính diện tích tam giác \(OAB\).
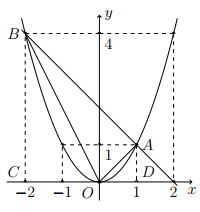
Gọi \(C\), \(D\)là hình chiếu của \(B\), \(A\) xuống \(Ox\). Ta có
\({S_{BCDA}} = \frac{{(BC + AD)CD}}{2} = \frac{{(4 + 1) \cdot 3}}{2} = \frac{{15}}{2},\)
\({S_{BCO}} = \frac{{BC \cdot CO}}{2} = 4\),
\({S_{ADO}} = \frac{{AD \cdot DO}}{2} = \frac{1}{2}\).
Suy ra
\({S_{ABO}} = {S_{BCDA}} - {S_{BCO}} - {S_{ADO}} = 3\).
Vậy diện tích tam giác \(OAB\)bằng 3 (đvdt).
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)Xem hình vẽ
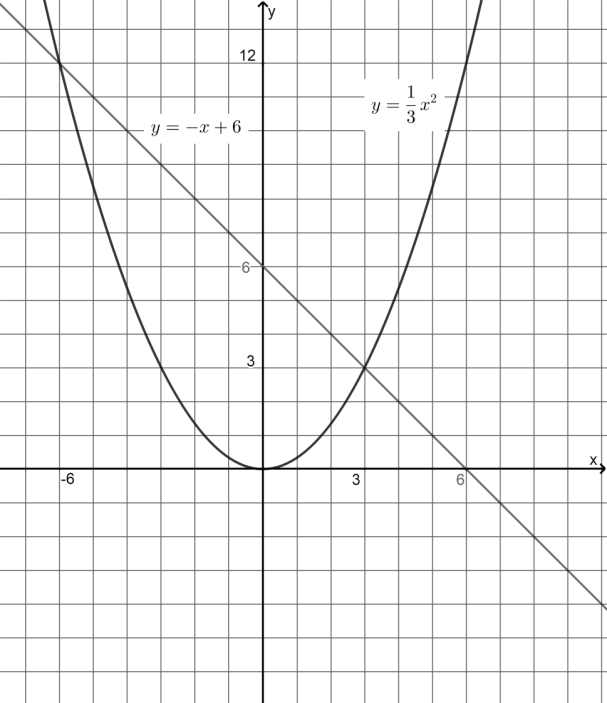
b) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình :
\(\frac{1}{3}{x^2} - - x + 6 \Leftrightarrow {x^2} + 3x - 18 = 0 \Leftrightarrow \left( {{x^2} - 9} \right) + (3x - 9) = 0\)
\( \Leftrightarrow (x - 3)(x + 3) + 3(x - 3) = 0 \Leftrightarrow (x - 3)(x + 6) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 3}\\{x = - 6}\end{array}} \right.\)
Với\(x = 3\,\) ta có \(y = \frac{1}{3} \cdot {3^2} = 3\)ta có giao điểm \[\left( {3;3} \right)\]
Với\(x = - 6\,\) ta có \(y = \frac{1}{3} \cdot {( - 6)^2} = 12\)ta có giao điểm \[\left( { - 6;12} \right)\]
Nhắn tin Zalo
Hỏi bài tập