Cho hình vẽ dưới đây:
![Cho hình vẽ dưới đây: Số đo góc \[ABC\] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/11-1769687163.png)
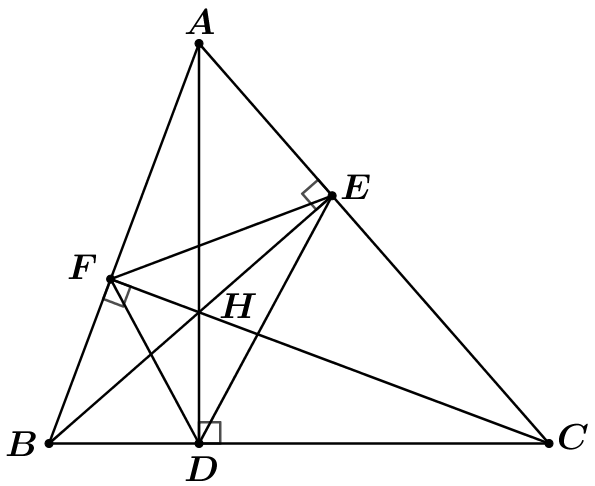
Số đo góc \[ABC\] là
Cho hình vẽ dưới đây:
![Cho hình vẽ dưới đây: Số đo góc \[ABC\] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/11-1769687163.png)
Số đo góc \[ABC\] là
Quảng cáo
Trả lời:
Chọn C
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh)
Đặt \(\widehat {BCE} = \widehat {DCF} = x\).
Theo tính chất góc ngoài tam giác, ta có:
\(\widehat {ABC} = \widehat {BCE} + \widehat E = x + 40^\circ \)
\(\widehat {ADC} = \widehat {DCF} + \widehat F = x + 20^\circ \)
Lại có \(\widehat {ABC} + \widehat {ADC} = 180^\circ \) (hai góc đối diện của tứ giác nội tiếp)
Suy ra \(\left( {x + 40^\circ } \right) + \left( {x + 20^\circ } \right) = 180^\circ \) hay \(x = 60^\circ \).
Do đó \(\widehat {ABC} = 60^\circ + 40^\circ = 100^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn B
Câu 2
Lời giải
Chọn B
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
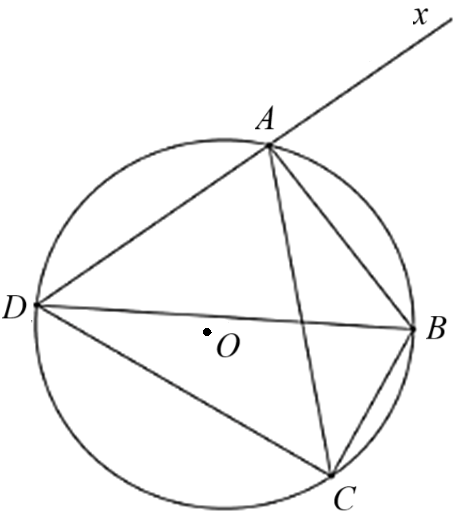
![Trong các hình vẽ tứ giác\[ABCD\]sau hãy chọn hình vẽ có tứ giác nội tiếp trong đường tròn. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/screenshot-5565-1769686463.png)