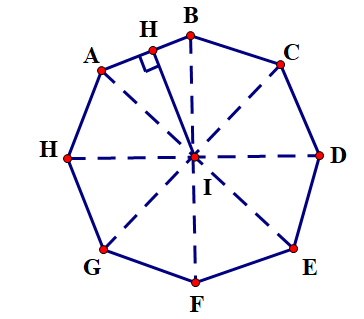
Đường viền ngoài của chiếc đồng hồ trong vẽ bên được làm theo hình đa giác đều nào? Tìm phép quay biến đa giác này thành chính nó.

Ta có \({\rm{AIB}} = 360^\circ :8 = 45^\circ \).

\(\Delta AIB\) cân tại \(I\) nên \(IAH = \frac{{180^\circ - AIB}}{2} = 67,5^\circ \).

Ta có \(H\) là trung điểm của \(AB\) ( \(\Delta AIB\) cân tại \(I;{\rm{ }}IH\) là đường cao nên \(IH\) cũng là đường trung tuyến) nên \(AH = \frac{{AB}}{2} = \frac{{25}}{2} = 12,5\left( {cm} \right)\).

Xét \(\Delta AIH\) vuông tại \(H:\tan IAH = \frac{{IH}}{{AH}} \Rightarrow IH = AH.\tan IAH = 12,5.\tan 67,5^\circ \left( {cm} \right)\).

Diện tích \(\Delta AIB\) là \(\frac{1}{2}.IH.AB = \frac{1}{2}.12,5.\tan 67,5^\circ .25 = 156,25.\tan 67,5^\circ \left( {c{m^2}} \right)\).

Diện tích bề mặt tấm thớt là \(\left( {156,25.\tan 67,5^\circ } \right).8 \approx 3017,8\left( {\;c{m^2}} \right)\)

Lưu ý: Số đo góc đáy của tam giác cân \( = \left( {180^\circ - } \right.\) số đo góc đỉnh cân) : 2