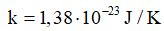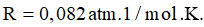Một nhóm học sinh tìm hiểu về sự phụ thuộc của lực từ tác dụng lên đoạn dây dẫn mang dòng điện đặt trong từ trường vào cường độ dòng điện chạy qua đoạn dây. Họ đã thực hiện các nội dung sau:
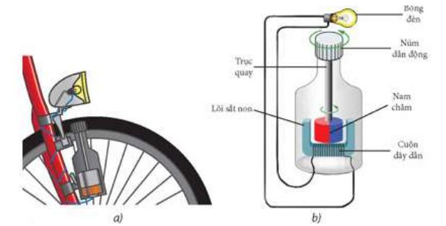
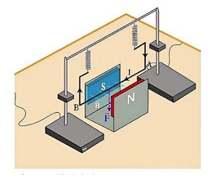
B1. Chuẩn bị các dụng cụ: Nam châm hình chữ \(U\), các khung dây dẫn mang dòng điện có khối lượng m , nguồn điện một chiều, ampe kế, hai lực kế giống hệt nhau (các dụng cụ đurợc mô phỏng như hình bên).
B2. Họ thảo luận và cho rằng khi làm thay đổi cường độ dòng điện qua đoạn dây dẫn thì độ lớn lực từ tác dụng lên đoạn dây sẽ thay đổi tỉ lệ thuận với cường độ dòng điện.
B3. Họ đã làm thí nghiệm thay đổi cuờng độ dòng điện chạy qua dây nhờ một biến trở và xác định lực từ tác dụng lên dây dẫn. Kết quả thu được cho thấy ti số giữa độ lớn lực từ F và cường độ dòng điện \(I\) là gần như không đổi.
Quảng cáo
Trả lời:
a) Đúng
b) Đúng
c) Sai. Vì chưa tính đến trọng lượng của dây
d) Đúng
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
\(r = \frac{d}{2} = \frac{{20}}{2} = 10\;{\rm{mm}}\)
\(\omega = \frac{v}{r} = \frac{{24/3,6}}{{10 \cdot {{10}^{ - 3}}}} = \frac{{2000}}{3}{\rm{rad}}/{\rm{s}}\)
\({E_0} = NBS\omega = 1500 \cdot {10^{ - 2}} \cdot 4 \cdot {10^{ - 4}} \cdot \frac{{2000}}{3} = 4\;{\rm{V}}\)
\(E = \frac{{{E_0}}}{{\sqrt 2 }} = \frac{4}{{\sqrt 2 }} = 2\sqrt 2 V\).Chọn DLời giải
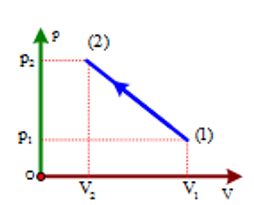
\({p_1}{V_1} = {p_2}{V_2} \Rightarrow {T_1} = {T_2} \Rightarrow {T_{{\rm{max }}}}\) tại trung điểm \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{p = \frac{{{p_1} + {p_2}}}{2} = \frac{{4,5 + 13,5}}{2} = 9\;{\rm{atm}}}\\{V = \frac{{{V_1} + {V_2}}}{2} = \frac{{18 + 6}}{2} = 12{\rm{l}}}\end{array}} \right.\)
\(\frac{{pV}}{{{T_{\max }}}} = nR \Rightarrow \frac{{9.12}}{{{T_{\max }}}} = 2.0,082 \Rightarrow {T_{\max }} \approx 658,5\;{\rm{K}}\)
\({W_d} = \frac{3}{2}kT = \frac{3}{2} \cdot 1,38 \cdot {10^{ - 23}} \cdot 658,5 \approx 1,36 \cdot {10^{ - 20}}J\)
Trả lời ngắn: 1,36
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.