Thả 12 viên nước đá vào một cốc cách nhiệt chứa \({\rm{m}}({\rm{g}})\) nước nóng \(80,{0^\circ }{\rm{C}}\) thì nhiệt độ cân bằng của nước là \(20,{0^\circ }{\rm{C}}\). Nhiệt dung riêng của nước là \(4180\;{\rm{J}}/{\rm{kg}}\). K, của nước đá \(2090\;{\rm{J}}/{\rm{kg}}\). K và nhiệt nóng chảy riêng của nước đá là \(3,33 \cdot {10^5}\;{\rm{J}}/{\rm{kg}}\). Các viên đá có khối lượng bằng nhau và có nhiệt độ \( - 10,{0^\circ }{\rm{C}}\). Nếu thả 9 viên nước đá vào cốc nước nói trên thì nhiệt độ cân bằng của nước trong cốc xấp xỉ
Quảng cáo
Trả lời:
\(\left\{ {\begin{array}{*{20}{l}}{12{m_d}\left( {{c_d}\Delta {t_d} + \lambda + {c_n}t} \right) = mc\left( {{t_n} - t} \right)}\\{9{m_d}\left( {{c_d}\Delta {t_d} + \lambda + {c_n}{t^\prime }} \right) = mc\left( {{t_n} - {t^\prime }} \right)}\end{array} \Rightarrow \frac{{12}}{9} \cdot \frac{{{c_d}\Delta {t_d} + \lambda + {c_n}t}}{{{c_d}\Delta {t_d} + \lambda + {c_n}{t^\prime }}} = \frac{{{t_n} - t}}{{{t_n} - {t^\prime }}}} \right.\)
\( \Rightarrow \frac{{12}}{9} \cdot \frac{{2090 \cdot 10 + 3,33 \cdot {{10}^5} + 4180 \cdot 20}}{{2090 \cdot 10 + 3,33 \cdot {{10}^5} + 4180 \cdot {t^\prime }}} = \frac{{80 - 20}}{{80 - {t^\prime }}} \Rightarrow {t^\prime } \approx 30,{5^\circ }C.{\rm{ }}\)Chọn B
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Câu 2
Lời giải
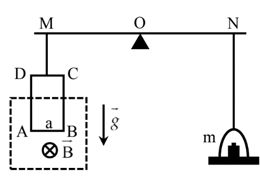
Cân ở trạng thái cân bằng \( \Rightarrow \) lực từ hướng xuống, cùng hướng trọng lực \( \Rightarrow \) a) Sai
Áp dụng quy tắc bàn tay trái \( \Rightarrow {\rm{i}}\) có chiều từ B tới \({\rm{A}} \Rightarrow \) b) Đúng
\(F = mg = 20 \cdot {10^{ - 3}} \cdot 9,8 = 0,196N = 196mN \Rightarrow \) c) Đúng
\(F = NIBl \Rightarrow 0,196 = 20.1 \cdot B \cdot 0,05 \Rightarrow B = 0,196T = 196mT \Rightarrow \) d) Đúng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
D. \(665\mu \;{\rm{W}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.