khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Tốt nghiệp THPT
  3. Vật lý

Câu hỏi:

02/02/2026 5,182 Lưu

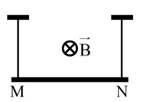
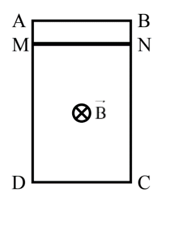
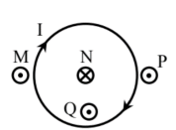
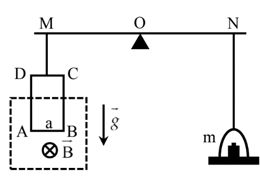
Hình vẽ mô tả thí nghiệm đo độ lớn của cảm ứng từ \(B\). Khung dây dẫn ABCD được gắn vào một cánh tay đòn OM của cân và được treo sao cho mặt phẳng khung vuông góc với vectơ cảm ứng từ của từ trường đều. Ban đầu, dòng điện trong khung dây bằng không, cân ở trạng thái cân bằng, đòn cân MN nằm ngang. Khi cho dòng điện có cường \({\rm{I}} = 1,0\;{\rm{A}}\) chạy qua khung dây thì cần thêm quả cân có khối lượng 20 g vào đĩa cân bên phải để cân trở lại trạng thái cân bằng, đòn cân MN nằm ngang. Khung dây hình chữ nhật ABCD gồm 20 vòng dây có chiều rộng \({\rm{AB}} = {\rm{a}} = 5,0\;{\rm{cm}}\). Lấy \({\rm{g}} = 9,8\;{\rm{m}}/{{\rm{s}}^2}\).

Hình vẽ mô tả thí nghiệm đo độ lớn của cảm ứng từ B.Khung dây dẫn ABCD được gắn vào một cánh tay đòn OM (ảnh 1)

a) Lực từ tác dụng vào khung dây ngược hướng với trọng lực của nó.
Đúng
Sai
b) Dòng điện I chạy trong khung dây có chiều từ B tới A.
Đúng
Sai
c) Độ lớn của lực từ tác dụng vào khung ABCD là 196 mN.
Đúng
Sai
d) Độ lớn của cảm ứng từ \({\rm{B}} = 196{\rm{mT}}\).
Đúng
Sai
Xem lời giải

Câu hỏi trong đề: Đề thi thử tốt nghiệp THPT môn Vật lí trường Lương Thế Vinh - Hà Nội có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Cân ở trạng thái cân bằng \( \Rightarrow \) lực từ hướng xuống, cùng hướng trọng lực \( \Rightarrow \) a) Sai

Áp dụng quy tắc bàn tay trái \( \Rightarrow {\rm{i}}\) có chiều từ B tới \({\rm{A}} \Rightarrow \) b) Đúng

\(F = mg = 20 \cdot {10^{ - 3}} \cdot 9,8 = 0,196N = 196mN \Rightarrow \) c) Đúng

\(F = NIBl \Rightarrow 0,196 = 20.1 \cdot B \cdot 0,05 \Rightarrow B = 0,196T = 196mT \Rightarrow \) d) Đúng

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

loading...

loading...

Đáp án  ____

Lời giải

Đáp án:

1. 1,2

\(e = Blv = 0,6 \cdot 0,2 \cdot 12 = 1,44\;{\rm{V}}\)

Mạch ngoài gồm \({R_{{\rm{NBAM }}}}//{R_{{\rm{NCDM }}}}\) (viết gọn \({{\rm{R}}_1}//{{\rm{R}}_2}\) )

\(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} \le \frac{{\frac{1}{4}{{\left( {{R_1} + {R_2}} \right)}^2}}}{{{R_1} + {R_2}}} = \frac{{{R_1} + {R_2}}}{4} = \frac{4}{4} = 1\Omega \)

\({i_{\min }} = \frac{e}{{{R_{\max }} + {R_{MN}}}} = \frac{{1,44}}{{1 + 0,2}} = 1,2A\)

Trả lời ngắn: 1,2

Câu 2

Treo một đoạn dây dẫn cứng MN , khối lượng m , bằng hai dây mảnh, nhẹ trong mặt phẳng thẳng đứng sao cho dây dẫn cân bằng nằm ngang trong từ trường đều như hình vẽ. Dòng điện trong dây dẫn MN có chiều từ N đến M và có giá trị không thay đổi. Cảm ứng từ có độ lớn \(B\) không đổi. Khi cảm ứng từ có hướng như hình vẽ thì lực căng của mỗi sợi dây có độ lớn là \({{\rm{T}}_1}\). Khi đổi ngược chiều từ trường thì khi dây dẫn MN cân bằng nằm ngang, lực căng mỗi dây có độ lớn là \({T_2}\) với \({T_1} = 2{T_2}\). Nếu vectơ cảm ứng từ có phương thẳng đứng thì khi thanh cân bằng, góc hợp bởi dây và phương thẳng đứng xấp xỉ

Treo một đoạn dây dẫn cứng MN , khối lượng m , bằng hai dây mảnh, nhẹ trong mặt phẳng thẳng đứng sao (ảnh 1)

 
A. \(45,{4^\circ }\)          
B. \(26,{5^\circ }\)  
C. \(63,{4^\circ }\)    
D. \(18,{4^\circ }\)

Lời giải

\({T_1} = 2{T_2} \Rightarrow P + F = 2(P - F) \Rightarrow \frac{F}{P} = \frac{1}{3} \Rightarrow \tan \alpha = \frac{1}{3} \Rightarrow \alpha \approx 18,{4^^\circ }.{\rm{ }}\)Chọn D

Câu 3

Hình bên diễn chiều cảm ứng từ tạo bởi dòng điện không đổi I chạy trong một vòng dây dẫn hình tròn tại các điểm nằm trong mặt phẳng dây dẫn. Tại điểm nào có kí hiệu không đúng với chiều của cảm ứng từ tại đó?

Hình bên diễn chiều cảm ứng từ tạo bởi dòng điện không đổi I chạy trong một vòng dây dẫn hình tròn tại các điểm nằm trong mặt phẳng dây dẫn. Tại điểm nào có kí hiệu không đúng với chiều của cảm ứng từ tại đó? (ảnh 1)
A. Điểm M.                  
B. Điểm Q.
C. Điểm N.       
  D. Điểm P.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong thí nghiệm tán xạ hạt alpha, bản chất hạt alpha là hạt nhân
A. \(_3^7{\rm{Li}}\)                             
B. \(_1^3{\rm{H}}\)                            
C. \(_7^{14}\;{\rm{N}}\)             
D. \(_2^4{\rm{He}}\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Thả 12 viên nước đá vào một cốc cách nhiệt chứa \({\rm{m}}({\rm{g}})\) nước nóng \(80,{0^\circ }{\rm{C}}\) thì nhiệt độ cân bằng của nước là \(20,{0^\circ }{\rm{C}}\). Nhiệt dung riêng của nước là \(4180\;{\rm{J}}/{\rm{kg}}\). K, của nước đá \(2090\;{\rm{J}}/{\rm{kg}}\). K và nhiệt nóng chảy riêng của nước đá là \(3,33 \cdot {10^5}\;{\rm{J}}/{\rm{kg}}\). Các viên đá có khối lượng bằng nhau và có nhiệt độ \( - 10,{0^\circ }{\rm{C}}\). Nếu thả 9 viên nước đá vào cốc nước nói trên thì nhiệt độ cân bằng của nước trong cốc xấp xỉ
A. \(25,{0^\circ }{\rm{C}}\)   
B. \(30,{5^\circ }{\rm{C}}\)  
C. \(65,{0^\circ }{\rm{C}}\)            
D. \(67,{5^\circ }{\rm{C}}\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một lượng khí lí tưởng được chứa trong bình kín có thể tích không đổi. Vào đầu buổi sáng, khí trong bình có áp suất bằng áp suất khí quyển \({{\rm{p}}_1} = {10^5}\;{\rm{Pa}}\), nhiệt độ \({{\rm{t}}_1} = {14^\circ }{\rm{C}}\). Tới giữa trưa, khí trong bình có áp suất \({{\rm{p}}_2}\), nhiệt độ \({{\rm{t}}_2} = {28^\circ }{\rm{C}}\). Nắp bình bị bật ra khi áp suất khí trong bình là 2. \({10^5}\;{\rm{Pa}}\) và khí thoát ra ngoài.
a) Khối lượng riêng của khí trong bình giảm dần khi nhiệt độ tăng từ \({14^\circ }{\rm{C}}\) tới \({28^\circ }{\rm{C}}\).
Đúng
Sai
b) Áp suất của khí trong bình tăng dần khi nhiệt độ tăng từ \({14^\circ }{\rm{C}}\) tới \({28^\circ }{\rm{C}}\).
Đúng
Sai
c) Tỉ số áp suất \({{\rm{p}}_2}/{{\rm{p}}_1}\) là 2.
Đúng
Sai
d) Khi nhiệt độ của khí trong bình bằng \({301^\circ }{\rm{C}}\) thì khí trong bình bắt đầu bị thoát ra ngoài.
Đúng
Sai

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập