Cho đồ thị hàm số \(y = {x^2}\) có đồ thị \(\left( P \right)\).
a) Vẽ đồ thị \(\left( P \right)\).
b) Tìm các điểm trên Parabol có tung độ bằng 16.
c) Tìm các điểm trên Parabol (khác gốc tọa độ) cách đều hai trục tọa độ.
Cho đồ thị hàm số \(y = {x^2}\) có đồ thị \(\left( P \right)\).
a) Vẽ đồ thị \(\left( P \right)\).
b) Tìm các điểm trên Parabol có tung độ bằng 16.
c) Tìm các điểm trên Parabol (khác gốc tọa độ) cách đều hai trục tọa độ.
Quảng cáo
Trả lời:
a)
- Bảng giá trị của \[y\] tương ứng với giá trị của \[x\] như sau:
|
\[x\] |
\[ - 2\] |
\[ - 1\] |
\[0\] |
\[1\] |
\[2\] |
|
\[y = {x^2}\] |
\[4\] |
\[1\] |
\[0\] |
\[1\] |
\[4\] |
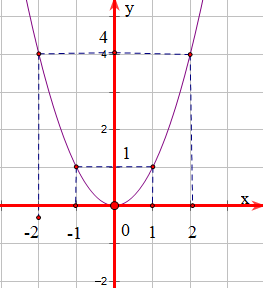
- Vẽ các điểm \[A\left( { - 2;4} \right),B\left( { - 1;1} \right),O\left( {0;0} \right),C\left( {1;1} \right),D\left( {2;4} \right)\] thuộc đồ thị hàm số \(y = {x^2}\) trong mặt phẳng \[Oxy\].
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số \(y = {x^2}\)
b) Gọi \(C\) là điểm thuộc \(\left( P \right)\) có tung độ bằng 16.
Ta có: \({y_C} = 16 \Leftrightarrow {x^2}_C = 16 \Leftrightarrow {x_C} = \pm 4\). Vậy \(C\left( {4;16} \right)\) hoặc \(C\left( { - 4;16} \right)\).
c) Gọi \(D\) là điểm thuộc \(\left( P \right)\) cách đều hai trục tọa độ.
Ta có: \(d\left( {D,Ox} \right) = \left| {{y_D}} \right| = x_D^2;d\left( {D,Oy} \right) = \left| {{x_D}} \right|\).
Theo giả thiết ta có: \(x_D^2 = \left| {{x_D}} \right| \Leftrightarrow \left| {{x_D}} \right| = 0\) (loại) hoặc \(\left| {{x_D}} \right| = 1\).
Vậy \(D\left( {1;1} \right)\) hoặc \(D\left( { - 1;1} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1. \((P)\) đi qua điểm \(A(1; - 2)\) khi và chỉ khi \( - 2 = a{.1^2} \Leftrightarrow a = - 2\).
2. Bảng giá trị

Lời giải
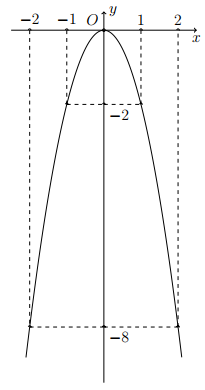
a)\(A( - \sqrt 2 ;4) \in (P) \Rightarrow 4 = a{\left( { - \sqrt 2 } \right)^2} \Rightarrow a = 2\)
Vậy \(a = 2\) là giá trị cần tìm.
b) Ta có \(y = 2{x^2}\)
+ Vẽ \(\left( P \right)\): Học sinh tự vẽ nhé
+ Thay \(y = 2\) vào hàm số \(y = 2{x^2}\) ta có:
\(\begin{array}{l}2 = 2{x^2}\\x = \pm 1\end{array}\)
\( \Rightarrow \left( {1;2} \right);\left( { - 1;2} \right)\)
+ Gọi \(M({x_0};{y_0}) \in (P) \Rightarrow {y_0} = 2x_{_0}^2\).
\(M\) cách đều \(Ox,\,\,Oy\) nên ta có:
\(\begin{array}{l}\left| {{x_0}} \right| = \left| {{y_0}} \right|\\\left| {{x_0}} \right| = \left| {2x_{_0}^2} \right|\\2x_{_0}^2 = \left| {{x_0}} \right|\end{array}\)
\(2x_{_0}^2 = - {x_0}\) hoặc \(2x_{_0}^2 = {x_0}\)
\(2x_{_0}^2 + {x_0} = 0\) hoặc \(2x_{_0}^2 - {x_0} = 0\)
\({x_0}\left( {2{x_0} + 1} \right) = 0\) hoặc \({x_0}\left( {2{x_0} - 1} \right) = 0\)
Giải \({x_0}\left( {2{x_0} + 1} \right) = 0\)
\({x_0} = 0\) hoặc \({x_0} = - \frac{1}{2}\)
Giải\({x_0}\left( {2{x_0} - 1} \right) = 0\)
\({x_0} = 0\) hoặc \({x_0} = \frac{1}{2}\)
Do đó \({x_0} \in \left\{ { - \frac{1}{2};0;\frac{1}{2}} \right\}\)
\( \Rightarrow {M_1}(0;0);{M_2}\left( {\frac{1}{2};\frac{1}{2}} \right);{M_3}\left( {\frac{{ - 1}}{2};\frac{1}{2}} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.