Cho tam giác nhọn \(ABC\) có đường cao \(AH\left( {H \in BC} \right)\) và nội tiếp đường tròn tâm \(O\) có đường kính \(AM\)(Hình vẽ). Chứng minh \(\widehat {OAC} = \widehat {BAH}\)
Cho tam giác nhọn \(ABC\) có đường cao \(AH\left( {H \in BC} \right)\) và nội tiếp đường tròn tâm \(O\) có đường kính \(AM\)(Hình vẽ). Chứng minh \(\widehat {OAC} = \widehat {BAH}\)
Câu hỏi trong đề: 15 bài tập Toán 9 Cánh diều Ôn tập chương 8 có đáp án !!
Quảng cáo
Trả lời:
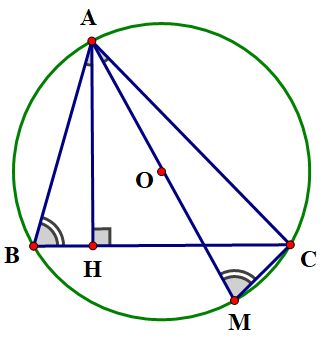
Dễ thấy (vì \(AM\) là đường kính). Tam giác \(ACM\) vuông tại
Lại có tam giác \(AHB\) vuông tại \(H\) (gt)
Mà \(\widehat {{\rm{AMC}}} = \widehat {{\rm{ABC}}}\) (góc nội tiếp cùng chắn cung)\( \Rightarrow \widehat {{\rm{OAC}}} = \widehat {{\rm{BAH}}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
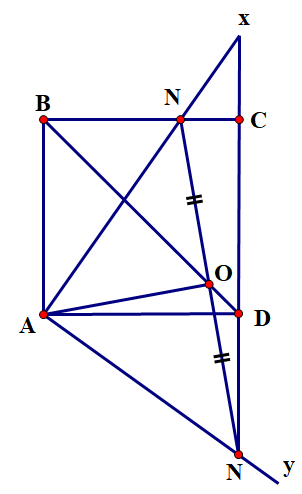
a) Ta có (1). Lại có \(Ax \bot Ay\) nên
Từ (1) và (2) \( \Rightarrow \widehat {{\rm{BAM}}} = \widehat {{\rm{DAN}}}\)nên hai tam giác vuông \(ABM\)và \(AND\)bằng nhau theo trường hợp g.c.g.
\( \Rightarrow {\rm{AM}} = {\rm{AN}}\)
b) Tam giác \(AMN\) vuông cân tại \(A\), có \(AO\) là đường trung tuyến nên đồng thời là đường cao hay \(AO \bot MN\) hay . Dễ thấy tứ giác \[ABMO\] có
nên \[ABMO\] là tứ giác nội tiếp.
Lại có , chứng tỏ bốn điểm \(A,O,D,N\) cùng thuộc một đường tròn đường kính \(AN\) hay tứ giác \[ANDO\]nội tiếp.
c) Ta có tứ giác\[\;ABMO\] nội tiếp (cmt) \( \Rightarrow \widehat {{\rm{BOM}}} = \widehat {{\rm{BAM}}}\) (góc nội tiếp cùng chắn cung ),\(\widehat {{\rm{BAM}}} = \widehat {{\rm{DAN}}}({\rm{cmt}})\). Lại có tứ giác \[ANDO\] nội tiếp (cmt) \( \Rightarrow \widehat {{\rm{DAN}}} = \widehat {{\rm{DON}}}\) (góc nội tiếp cùng chắn cung)
\( \Rightarrow \widehat {{\rm{BOM}}} = \widehat {{\rm{DON}}}\), mà ba điểm \(M,O,N\) thẳng hàng (gt)\( \Rightarrow B,D,O\)thẳng hàng.
Lời giải
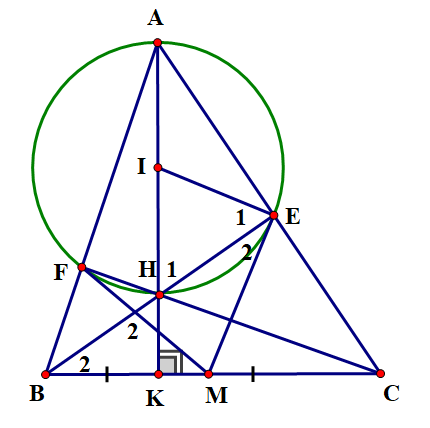
a) Dễ thấy (gt).
Tứ giác \[AEHF\] có (gt) nên nội tiếp đường tròn tâm \(I\).
b) Ta có tam giác \(BEC\) vuông tại \(E\) (gt), \(EM\) là trung tuyến
\( \Rightarrow EM = BM = CM\) hay cân tại M \[ \Rightarrow \widehat {{B_2}} = \widehat {{E_2}}\]
Lại có \(H,E\) thuộc đường tròn tâm \(I\) nên cân tại I \( \Rightarrow \widehat {{H_2}} = \widehat {{E_1}}\) mà \(\widehat {{H_1}} = \widehat {{H_2}}\) (đối đỉnh) \( \Rightarrow \widehat {{E_1}} = \widehat {{H_2}}\)
Gọi K là chân đường cao kẻ từ A đến BC, ta có tam giác BKH vuông tại K
Gọi K là chân đường cao kẻ từ A đến BC, ta có tam giác BKH vuông tại K
Chứng tỏ \(ME\) tiếp xúc với đường tròn \(\left( I \right)\)ngoại tiếp tứ giác \[AEHF\].
Chứng minh tương tự ta có \(MF\) tiếp xúc với \(\left( I \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.