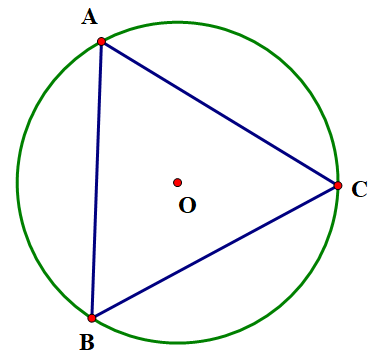
Cho ngũ giác \[ABCDE\]có các cạnh bằng nhau và \(\widehat A = \widehat B = \widehat C\).
a) Chứng minh tứ giác \[ABCD\]là hình thang cân.
b) Chứng minh ngũ giác \[ABCDE\]là ngũ giác đều.
Cho ngũ giác \[ABCDE\]có các cạnh bằng nhau và \(\widehat A = \widehat B = \widehat C\).
a) Chứng minh tứ giác \[ABCD\]là hình thang cân.
b) Chứng minh ngũ giác \[ABCDE\]là ngũ giác đều.
Câu hỏi trong đề: 18 bài tập Toán 9 Cánh diều Ôn tập chương 9 có đáp án !!
Quảng cáo
Trả lời:

a) \(\Delta ABC\)và \(\Delta BCD\)có \(AB = BC\);\(\widehat {ABC} = \widehat {BCD}\);\(BC = CD\)
\( \Rightarrow \Delta ABC = \Delta BCD\left( {c.g.\,c} \right)\)\( \Rightarrow AC = BD\).
\(\Delta ABD\)và \(\Delta ACD\)có \(AB = DC\);\(AC = DB\); AD chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c.g.\,c} \right)\)\( \Rightarrow \widehat {BAD} = \widehat {CDA}\)
\( \Rightarrow \Delta BAH = \Delta CDK\)\( \Rightarrow BH = CK\)\( \Rightarrow BC\,{\rm{//}}\,{\rm{CD}}\)
\( \Rightarrow {\rm{ABCD}}\,\)là hình thang cân
b) Chứng minh tương tự câu a, ta có \[ABCE\]là hình thang cân.
Ta có: \(\Delta ABC\)cân\( \Rightarrow \widehat {BAC} = \widehat {BCA}\),mà \(\widehat A = \widehat C\)\( \Rightarrow \widehat {CAE} = \widehat {ACD}\)
\( \Rightarrow \Delta AEC = \Delta CDA\left( {c.g.\,c} \right)\)\( \Rightarrow ACDE\)là hình thang cân
(Chứng minh tương tự câu a)
Ta có:
\(AB\,{\rm{//}}\,{\rm{CK}}\)(\[ABCD\] là hình thang cân)
\({\rm{BC}}\,{\rm{//}}\,{\rm{AK}}\)(\[ABCE\] là hình thang cân)
mà: \(AB = BC\). Suy ra \[ABCK\]là hình thoi\( \Rightarrow \widehat {{A_1}} = \widehat {{C_1}} = \widehat {{C_2}}\)
\[ACDE\]là hình thang cân\( \Rightarrow \widehat {{C_2}} = \widehat {{E_1}}\)\( \Rightarrow \widehat {{E_1}} = \widehat {{C_1}}\)\( \Rightarrow \widehat {{C_1}} = \widehat {{C_3}}\)
\( \Rightarrow \Delta ABC = \Delta CDE\)\( \Rightarrow \widehat {ABC} = \widehat {CDE}\)
Chứng minh tương tự, ta được: \(\widehat {BAE} = \widehat {AED}\)
Do đó: \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)và \(AB = BC = CD = DE = EA\left( {gt} \right)\)
\( \Rightarrow ABCDE\)là ngũ giác đều
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
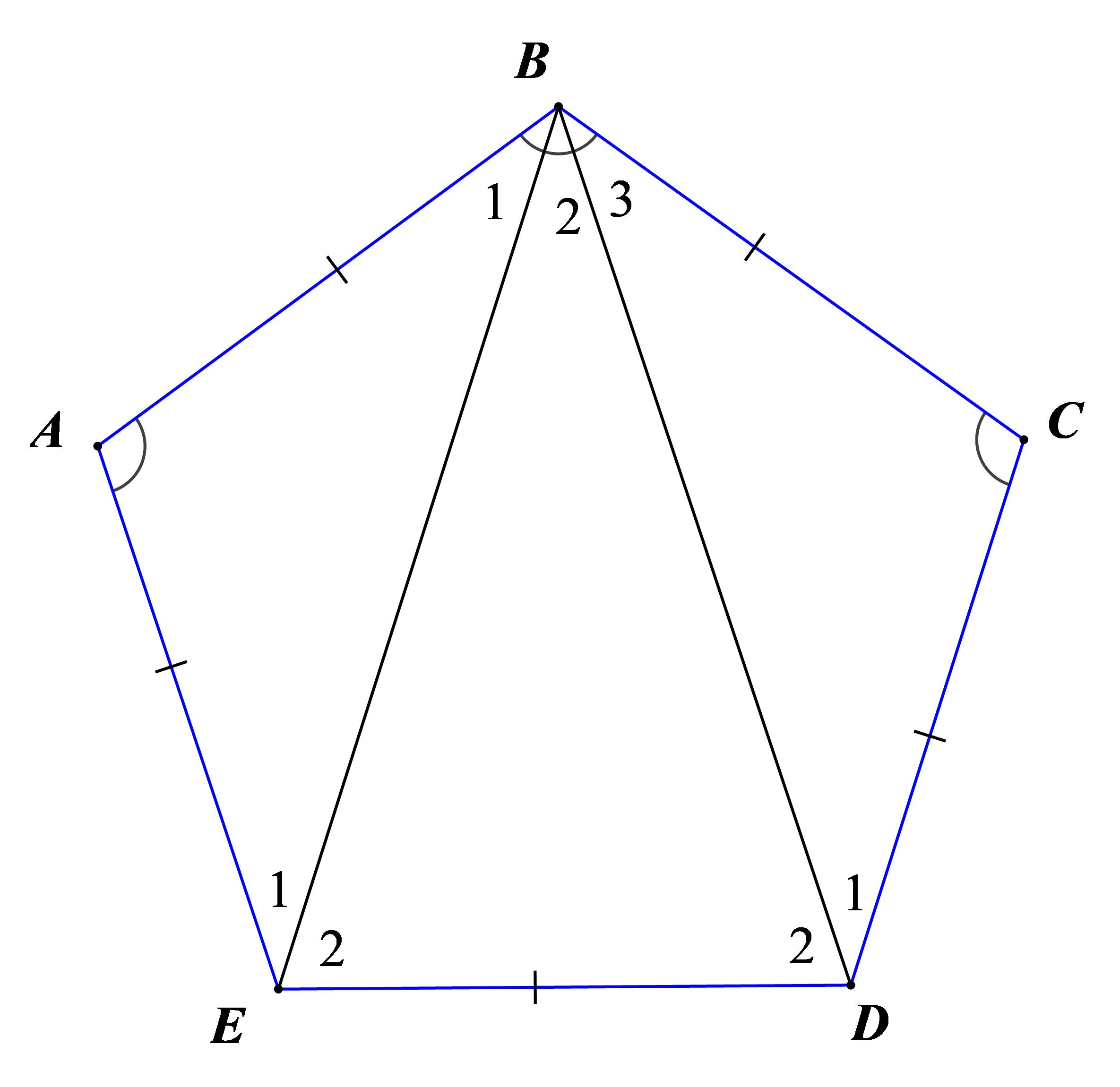
Ta có : \(AB = BC = CD = DE = EA\,\,\left( {gt} \right)\,\,\left( * \right)\)
Xét tam giác \(ABE\) có \(AB = AE\,\,\) (gt)
Nên \(\Delta ABE\) cân tại A có \(\widehat A = 108^\circ \)
\( \Rightarrow {\widehat B_1} = {\widehat E_1} = \frac{{180^\circ - \widehat A}}{2} = \frac{{180^\circ - 108^\circ }}{2} = 36^\circ \)
Tương tự với tam giác \(BCD\), ta có : \({\widehat B_3} = {\widehat D_1} = 36^\circ \)
Lại có \(\widehat {ABC} = {\widehat B_1} + {\widehat B_2} + {\widehat B_3} = 108^\circ \)
\( \Rightarrow {\widehat B_2} = 108^\circ - \left( {{{\widehat B}_1} + {{\widehat B}_3}} \right) = 108^\circ - \left( {36^\circ + 36^\circ } \right) = 36^\circ \)
Dễ thấy \(\Delta ABE = \Delta CBD\,\,\left( {c.g.c} \right)\)
Lời giải
a) Phép quay ngược chiều 72o tâm O biến điểm A biến B thì các điểm \(B,C,D,E\) lần lượt biến thành các điểm \(C,D,E\)và A .
b) Ba phép quay tâm O giữ nguyên hình ngũ giác đều:
1. Phép quay ngược chiều 144o;
2. Phép quay ngược chiều 216o;
3. Phép quay thuận chiều 72o.
Bạn hãy tìm thêm những phép quay còn lại giữ nguyên hình ngũ giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hình ngũ giác đều \[ABCDE\]có tâm \(O\) (Hình vẽ). a) Phép quay ngược chiều tâm O biến điểm A thành điểm B thì các điểm \(B,C,D,E\) tương ứng biến thành các điểm nào? b) Chỉ ra ba phép quay tâm O giữ nguyên hình ngũ giác đều đã cho. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/19-1769711285.png)