Một hình trụ \[\left( T \right)\] được tạo ra khi quay hình chữ nhật \[ABCD\] một vòng quanh cạnh \[AB.\] Biết \[AC = 2a\sqrt 2 \] và \[\widehat {ACB} = 45^\circ .\] Thể tích \[V\] của hình trụ \[\left( T \right)\] là
A. \[V = 16\pi {a^3}.\]
B. \[V = 8\pi {a^3}.\]
C. \[V = 4\pi {a^3}.\]
D. \[V = 12\pi {a^3}.\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
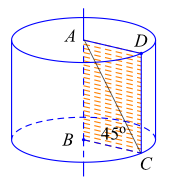
Vì \[ABCD\] là hình chữ nhật nên \[AB \bot BC.\]
Vì tam giác \[ABC\] vuông tại \[B\] nên:
⦁ \[AB = AC \cdot \sin \widehat {ACB} = 2a\sqrt 2 \cdot \sin 45^\circ = 2a.\]
⦁ \[BC = AC \cdot \cos \widehat {ACB} = 2a\sqrt 2 \cdot \cos 45^\circ = 2a.\]
Thể tích \[V\] của hình trụ \[\left( T \right)\] là:
\[V = \pi {r^2}h = \pi \cdot B{C^2} \cdot AB = \pi \cdot {\left( {2a} \right)^2} \cdot 2a = 8\pi {a^3}.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[96\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
B. \[110\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
C. \[112\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
D. \[128\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Lời giải
Chọn D
Bán kính đáy của hộp sữa là: \[r = \frac{d}{2} = \frac{8}{2} = 4{\rm{\;(cm)}}{\rm{.}}\]
Diện tích toàn phần của hộp sữa là:
\[{S_{tp}} = 2\pi r\left( {h + r} \right) = 2\pi \cdot 4\left( {12 + 4} \right) = 128\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Câu 2
A. \[27,25{\rm{\;cm}}.\]
B. \[32,25{\rm{\;cm}}.\]
C. \[70,5{\rm{\;cm}}.\]
D. \[{\rm{54,5\;cm}}.\]
Lời giải
Chọn A
Gọi chiều cao của hình trụ là \(h{\rm{\;(cm)}}{\rm{.}}\)
Công thức tính diện tích toàn phần của hình trụ là \[{S_{tp}} = 2\pi r\left( {h + r} \right)\]
Suy ra: \[2\pi \cdot 8\left( {h + 8} \right) = 564\pi \]
Nên \[h + 8 = 35,25\]
Do đó \[h = 27,25{\rm{\;(cm)}}{\rm{.}}\]
Câu 3
A. \[V = \frac{4}{3}\pi {r^2}h.\]
B. \[V = \frac{2}{3}\pi {r^2}h.\]
C. \[V = \pi {r^2}h.\]
D. \[V = \frac{1}{3}\pi {r^2}h.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
![Câu 14: Cho hình trụ nằm bên trong hình lập phương có cạnh bằng \[x\] (hình vẽ). Tỉ số thể tích của hình trụ và hình lập phương đã cho là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/6-1769741894.png)
A. \[\frac{\pi }{2}.\]
B. \[\frac{\pi }{4}.\]
C. \[\frac{\pi }{{12}}.\]
D. \[\frac{{2\pi }}{3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[{S_{tp}} = \pi rl + \pi {r^2}.\]
B. \[{S_{tp}} = 2\pi rh + 2\pi {r^2}.\]
C. \[{S_{tp}} = \pi rh + \pi {r^2}.\]
D. \[{S_{tp}} = \pi rl + 2\pi {r^2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. gấp 4 lần thể tích cũ.
B. gấp 8 lần thể tích cũ.
C. gấp 12 lần thể tích cũ.
D. gấp 16 lần thể tích cũ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[\frac{8}{3}{\rm{\;cm}}.\]
B. \[\frac{{4\sqrt 3 \pi }}{3}{\rm{\;cm}}.\]
C. \[\frac{{4\pi }}{3}{\rm{\;cm}}.\]
D. \[\frac{{8\pi }}{3}{\rm{\;cm}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập