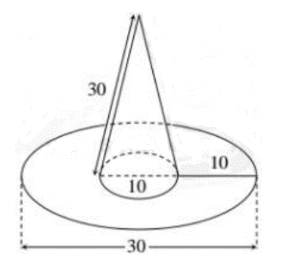
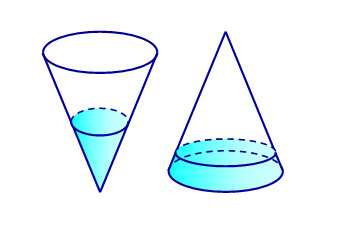
Một chiếc thùng chứa đầy nước có hình một khối lập phương. Đặt vào trong thùng đó một khối nón sao cho đỉnh khối nón trùng với tâm một mặt của khối lập phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện. Tính tỉ số thể tích của lượng nước trào ra ngoài và lượng nước còn lại ở trong thùng.
Một chiếc thùng chứa đầy nước có hình một khối lập phương. Đặt vào trong thùng đó một khối nón sao cho đỉnh khối nón trùng với tâm một mặt của khối lập phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện. Tính tỉ số thể tích của lượng nước trào ra ngoài và lượng nước còn lại ở trong thùng.
Câu hỏi trong đề: 20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Coi khối lập phương có cạnh \[1\]. Thể tích khối lập phường là \[V = 1\].
Từ giả thiết ta suy ra khối nón có chiều cao \[h = 1\], bán kính đáy \[r = \frac{1}{2}\].
Thể tích lượng nước trào ra ngoài là thể tích \[{V_1}\] của khối nón.
Ta có: \[{V_1} = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .\frac{1}{4}.1 = \frac{\pi }{{12}}\].
Thể tích lượng nước còn lại trong thùng là: \[{V_2} = V - {V_1} = 1 - \frac{\pi }{{12}} = \frac{{12 - \pi }}{{12}}\].
Do đó: \[\frac{{{V_1}}}{{{V_2}}} = \frac{\pi }{{12 - \pi }}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vì chiếc nón hình nón có bán kính đáy R = 28: 2 = 14cm và đường sinh l = 30cm nên diện tích xung quanh của chiếc nón là:
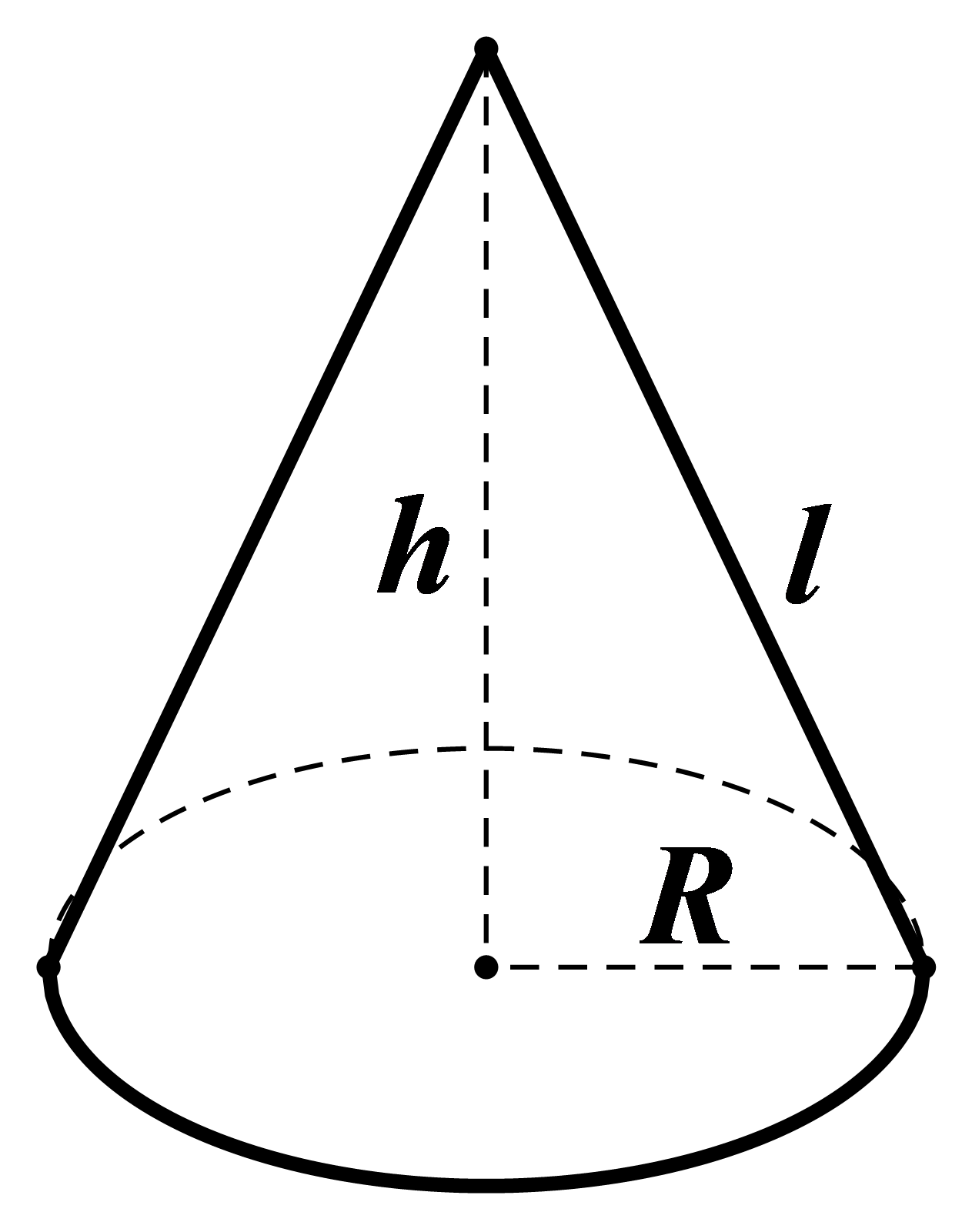
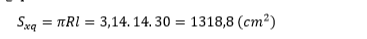
Vậy diện tích lá dùng để làm nón là 110%.1318,8=1450,68 cm2
Lời giải
Vì chiếc nón hình nón có đường sinh l = 30cm và bán kính đáy R = 40: 2 = 20cm nên diện tích xung quanh của chiếc nón là:
Sxq = pRl = p. 20. 30 = 600p (cm2)
diện tích là cần dùng cho một chiếc nón là: 2. 600p = 1200p cm2.
Vậy diện tích là cần dùng làm 5000 chiếc nón là: 500. 1200p = 600000p cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập